
【题目】如图,在三棱台ABC-A1B1C1中,底面ABC是边长为2的等边三角形,上、下底面的面积之比为1:4,侧面A1ABB1⊥底面ABC,并且A1A=A1B1,∠AA1B=90°.
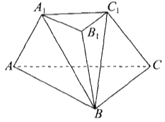
(1)平面A1C1B∩平面ABC=l,证明:A1C1∥l;
(2)求四棱锥B-A1ACC1的体积.
【答案】(1)见解析(2)![]()
【解析】
(1)三棱台中上底面与下底面是平行的,即平面A1B1C1∥平面ABC,再由面面平行的性质定理可以得到;
(2) 取AB中点O,连接CO,则CO⊥AB,由面面垂直的性质可得CO⊥平面A1ABB1,由已知求得上底面边长,然后利用等积法求四棱锥B-A1ACC1的体积.
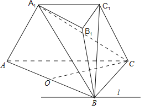
(1)证明:如图,∵平面A1B1C1∥平面ABC,
且平面A1C1B∩平面ABC=l,A1C1B∩平面A1B1C1=A1C1,
∴A1C1∥l;
(2)解:∵底面ABC是等边三角形,取AB中点O,
连接CO,则CO⊥AB,
∵面A1ABB1⊥底面ABC,且面A1ABB1∩底面ABC=AB,
∴CO⊥平面A1ABB1,连接A1C,
在三棱台ABC-A1B1C1中,
∵上、下底面的面积之比为1:4,∴AB=2A1B1,
由AB=2,得CO=![]() ,A1B1=1,则A1A=A1B1=1,
,A1B1=1,则A1A=A1B1=1,
又∠AA1B=90°,∴![]() ,
,
则![]() ,
,
∴![]() =
=![]() ;
;
由AC=2A1C1,得![]() ,
,
∴![]() ,
,
∴四棱锥B-A1ACC1的体积![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的序号是( )
①函数f(x)在定义域R内可导,“f′(1)=0”是“函数f(x)在x=1处取极值”的充分不必要条件;
②函数f(x)=x3![]() ax在[1,2]上单调递增,则a≥﹣4
ax在[1,2]上单调递增,则a≥﹣4
③在一次射箭比赛中,甲、乙两名射箭手各射箭一次.设命题p:“甲射中十环”,命题q:“乙射中十环”,则命题“至少有一名射箭手没有射中十环”可表示为(¬p)∨(¬q);
④若椭圆![]() 左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
A.①③④B.②③④C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 过点
过点![]() 且与直线
且与直线![]() 垂直,直线
垂直,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,动点
轴对称,动点![]() 满足
满足![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,问
,问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
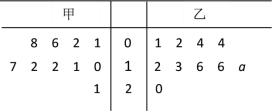
【题目】为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a表示.
(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值, 求图中a的所有可能取值;
(Ⅱ)将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设![]() ,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
(Ⅲ)记甲组阅读量的方差为![]() . 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为
. 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为![]() ;若A的阅读量为20,则记新甲组阅读量的方差为
;若A的阅读量为20,则记新甲组阅读量的方差为![]() ,试比较
,试比较![]() ,
,![]() ,
,![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海市旅游节刚落下帷幕,在旅游节期间,甲、乙、丙三位市民顾客分别获得一些景区门票的折扣消费券,数量如表1,已知这些景区原价和折扣价如表2(单位:元).
表1:
数量 | 景区1 | 景区2 | 景区3 |
甲 | 0 | 2 | 2 |
乙 | 3 | 0 | 1 |
丙 | 4 | 1 | 0 |
表2:
门票 | 景区1 | 景区2 | 景区3 |
原价 | 60 | 90 | 120 |
折扣后价 | 40 | 60 | 80 |
(1)按照上述表格的行列次序分别写出这三位市民获得的折扣消费券数量矩阵A和三个景区的门票折扣后价格矩阵B;
(2)利用你所学的矩阵知识,计算三位市民各获得多少元折扣?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com