
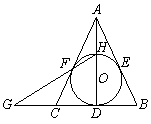
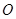 的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,
的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,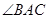 的平分线与BC和圆
的平分线与BC和圆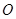 分别交于点D和E。
分别交于点D和E。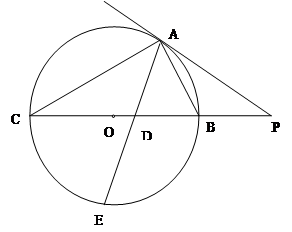
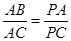 ;
;( II)先根据切割线定理得到PA2=PB•PC;结合第一问的结论以及勾股定理求出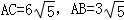 ;再结合条件得到△ACE∽△ADB,进而求出结果. ;再结合条件得到△ACE∽△ADB,进而求出结果. |
| 解:( I)∵PA为⊙O的切线, ∴∠PAB=∠ACP,…(1分) 又∠P公用,∴△PAB∽△PCA.…(2分) ∴  .…(3分) .…(3分)( II)∵PA为⊙O的切线,PBC是过点O的割线, ∴PA2=PB•PC.…(5分) 又∵PA=10,PB=5,∴PC=20,BC=15.…(6分) 由( I)知, 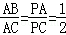 , ,∵BC是⊙O的直径, ∴∠CAB=90°. ∴AC2+AB2=BC2=225, ∴ 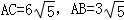 …(7分) …(7分)连接CE,则∠ABC=∠E,…(8分) 又∠CAE=∠EAB, ∴△ACE∽△ADB, ∴ 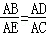 …(9分) …(9分)∴ 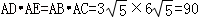 .…(10分) .…(10分) |


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
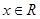 ,
,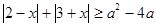 恒成立,则
恒成立,则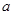 满足________.
满足________.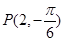 到直线
到直线 :
: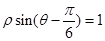 的距离是_______.
的距离是_______.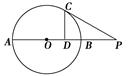
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
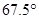 的角的正切值是 .
的角的正切值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com