
分析 把已知圆的方程化为标准方程后,找出圆心坐标和半径r,利用两点间的距离公式求出点到圆心的距离d,过点(1,2)可作圆x2+y2+2x-4y+k-2=0的两条切线,可得P在圆外,即P到圆心的距离d大于圆的半径r,令d大于r列出关于k的不等式,同时考虑7-k大于0,两不等式求出公共解集即可得到k的取值范围.
解答 解:把圆的方程化为标准方程得:(x+1)2+(y-2)2=7-k,
∴圆心坐标为(-1,2),半径r=$\sqrt{7-k}$,
则点(1,2)到圆心的距离d=2,
由题意可知点(1,2)在圆外时,过点(1,2)总可以向圆x2+y2+2x-4y+k-2=0作两条切线,
∴d>r即$\sqrt{7-k}<2$,且7-k>0,解得:3<k<7,
则k的取值范围是(3,7).
故答案为:(3,7).
点评 本题考查了点与圆的位置关系的判别方法,灵活运用两点间的距离公式化简求值,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{3π}{4}$] | B. | [0,$\frac{π}{4}$] | C. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | D. | [$\frac{π}{4}$,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲一定在画画 | B. | 甲一定在听音乐 | C. | 乙一定不看书 | D. | 丙一定不画画 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
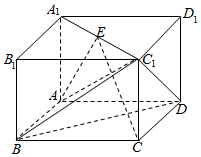 在长方体ABCD-A1B1C1D1中,E是A1C1与B1D1的交点,AB=BC=$\sqrt{2}$,AA1=1.
在长方体ABCD-A1B1C1D1中,E是A1C1与B1D1的交点,AB=BC=$\sqrt{2}$,AA1=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某房子屋檐A点离地面15米.房子上另一点B离地面9米,而且A,B两点在同一铅垂线上,在离地面7米的C处看此房子,问水平距离离此房子多远时A,B的视角(∠ACB)最大?
如图,某房子屋檐A点离地面15米.房子上另一点B离地面9米,而且A,B两点在同一铅垂线上,在离地面7米的C处看此房子,问水平距离离此房子多远时A,B的视角(∠ACB)最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,$\frac{5}{3}$] | B. | [-5,0)∪[$\frac{5}{3}$,+∞) | C. | (-∞,-5]∪[$\frac{5}{3}$,+∞) | D. | [-5,0)∪(0,$\frac{5}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com