
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求a的值,并证明![]() 是R上的增函数;
是R上的增函数;
(2)若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,定义
,定义![]() (
(![]() ,且
,且![]() 为常数),若
为常数),若![]() ,
,![]() ,
,![]() .以下四个命题中为真命题的是__________.
.以下四个命题中为真命题的是__________.
①![]() 不存在极值;②若
不存在极值;②若![]() 的反函数为
的反函数为![]() ,且函数
,且函数![]() 与函数
与函数![]() 有两个公共点,则
有两个公共点,则![]() ;③若
;③若![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是
的取值范围是![]() ;④若
;④若![]() ,则在
,则在![]() 的曲线上存在两点,使得过这两点的切线互相垂直.
的曲线上存在两点,使得过这两点的切线互相垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份之间的回归直线方程
与月份之间的回归直线方程![]() ;
;
(2)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下![]() 列联表:能否据此判断有
列联表:能否据此判断有![]() 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
参考公式及数据:
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与
与![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,与直线
,与直线![]() 相交于
相交于![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() 均不重合).证明:
均不重合).证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道一次函数、二次函数的图像都是连续不断的曲线,事实上,多项式函数的图像都是如此.
(1)设![]() ,且
,且![]() ,若还有
,若还有![]() ,求证:
,求证:![]() ;
;
(2)设一个多项式函数有奇次项![]() (
(![]() ),求证:总能通过只调整
),求证:总能通过只调整![]() 的系数,使得调整后的多项式一定有零点;
的系数,使得调整后的多项式一定有零点;
(3)现有未知数为![]() 的多项式方程
的多项式方程![]() (其中实数
(其中实数![]() 待定),甲、乙两人进行一个游戏:由甲开始交替确定
待定),甲、乙两人进行一个游戏:由甲开始交替确定![]() 中的一个数(每次只能去确定剩余还未定的数),当甲确定最后一个数后,若方程由实数解,则乙胜,反之甲胜,问:乙有必胜的策略吗?若有,请给出策略并证明,若无,请说明理由.
中的一个数(每次只能去确定剩余还未定的数),当甲确定最后一个数后,若方程由实数解,则乙胜,反之甲胜,问:乙有必胜的策略吗?若有,请给出策略并证明,若无,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数![]() 随时刻
随时刻![]() (时)变化的规律满足表达式
(时)变化的规律满足表达式![]() ,
,![]() ,其中
,其中![]() 为空气治理调节参数,且
为空气治理调节参数,且![]() .
.
(1)令![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若规定每天中![]() 的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数
的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格.某校有800 名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
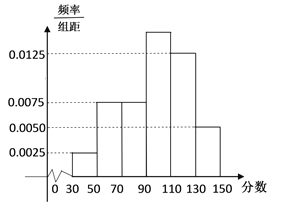
(Ⅰ)求初赛分数在区间![]() 内的频率;
内的频率;
(Ⅱ)求获得复赛资格的人数;
(Ⅲ)据此直方图估算学生初赛成绩的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.
两侧的动点.
①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com