选修4-5:不等式选讲已知实数a,b,c满足a2+2b2+3c2=24
①求a+2b+3c的最值;
②若满足题设条件的任意实数a,b,c,不等式a+2b+3c>|x+1|-14恒成立,求实数x的取值范围.
解:①因为已知a、b、c是实数,且a
2+2b
2+3c
2=24
根据柯西不等式(a
2+b
2+c
2)(x
2+y
2+z
2)≥(ax+by+cz)
2故有(a
2+2b
2+3c
2)(1
2+
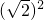
+(

)
2)≥(a+2b+3c)
2故(a+2b+3c)
2≤144,即|a+2b+3c|≤12
即a+2b+3c的最大值为12,a+2b+3c的最小值为-12;
②:已知不等式a+2b+3c>|x+1|-14恒成立,即需要|x+1|-14小于a+2b+3c的最小值即可.
即|x+1|-14<-12.解得:-2<x+1<2,-3<x<1
即:实数x的取值范围(-3,1).
分析:①首先分析题目已知a
2+2b
2+3c
2=24,求a+2b+3c的最大值,考虑到柯西不等式(a
2+b
2+c
2)(x
2+y
2+z
2)≥(ax+by+cz)
2的应用,构造出柯西不等式求出(a+2b+3c)
2的最大值开方即可得到答案.
②首先分析题目已知不等式a+2b+3c>|x+1|-14恒成立,求x的取值范围,即需要k小于|x+1|+|x-2|的最小值即可.由①分析得a+2b+3c的最小值,即|x+1|-14<-1可得到答案.
点评:此题主要考查一般形式的柯西不等式的应用,对于此类题目很多同学一开始就想到应用球的参数方程求解,这个方法可行但是计算量较高,而应用柯西不等式求解较简单,同学们需要很好的理解掌握.此题还考查不等式恒成立的问题.

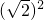 +(
+( )2)≥(a+2b+3c)2
)2)≥(a+2b+3c)2

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案