Question

18．利用三角函数线，求满足下列条件的α的范围．
（1）sinα＜-$\frac{1}{2}$；
（2）cosα＞$\frac{\sqrt{3}}{2}$．

Answer 1

分析 由已知条件作出单位圆，结合单位圆找出[0，2π）内α的范围，由此利用终边相同的角的概念能求出满足条件的α的范围．

解答 解：（1）∵sinα＜-$\frac{1}{2}$，
∴作出单位圆如下图：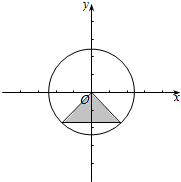

由单位图得到$\frac{7π}{6}$＜α＜$\frac{11π}{6}$，
∴满足sinα＜-$\frac{1}{2}$的α的范围是{α|2k$π+\frac{7π}{6}$＜α＜2kπ+$\frac{11π}{6}$，k∈Z}．
（2）∵cosα＞$\frac{\sqrt{3}}{2}$，
∴作出单位圆如下图：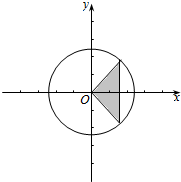

由单位图得到$\frac{11π}{6}$＜α＜2π，或0≤α＜$\frac{π}{6}$，
∴满足cosα＞$\frac{\sqrt{3}}{2}$的α的范围是{α|2kπ≤α＜2kπ+$\frac{π}{6}$，或2k$π+\frac{11π}{6}$＜α＜2kπ+2π，k∈Z}．

点评 本题考查满足条件的角的取值范围的求法，是基础题，解题时要认真审题，注意单位圆的性质的合理运用．