
【题目】在某校矩形的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在![]() 范围内,规定分数在80以上(含80)的同学获奖,按文理科用分层抽样的放发抽取200人的成绩作为样本,得到成绩的频率分布直方图.
范围内,规定分数在80以上(含80)的同学获奖,按文理科用分层抽样的放发抽取200人的成绩作为样本,得到成绩的频率分布直方图.
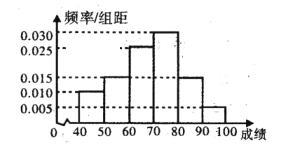
(Ⅰ)填写下面![]() 的列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”;
的列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”;
(Ⅱ)将上述调查所得的频率视为概率,现从参赛学生中,任意抽取3名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

附表及公式:![]() ,其中
,其中![]()

科目:高中数学 来源: 题型:
【题目】已知集合A={x|3≤![]() ≤27},B={x|
≤27},B={x|![]() >1}.
>1}.
(1)分别求A∩B,(![]() )∪A;
)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD= ![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点. 
(Ⅰ)证明:平面EAC⊥平面PBD;
(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(2,![]() ),且倾斜角α=
),且倾斜角α=![]() ,曲线C:
,曲线C:![]() (θ为参数),直线l与曲线C相交于不同的两点A,B.
(θ为参数),直线l与曲线C相交于不同的两点A,B.
(1)写出直线![]() 的参数方程,及曲线C的普通方程;
的参数方程,及曲线C的普通方程;
(2)求线段AB的中点Q的坐标,及![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺作样本,检测其某项质量指标,检测结果如频率分布直方图所示.

(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() 和方差
和方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若该品牌的速冻水饺的某项质量指标Z服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①求Z落在![]() 内的概率;
内的概率;
② 若某人从某超市购买了1包这种品牌的速冻水饺,发现该包速冻水饺某项质量指标值为55,根据![]() 原则判断该包速冻水饺某项质量指标值是否正常
原则判断该包速冻水饺某项质量指标值是否正常
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知P(x0 , y0)是椭圆C: ![]() =1上一点,过原点的斜率分别为k1 , k2的两条直线与圆(x﹣x0)2+(y﹣y0)2=
=1上一点,过原点的斜率分别为k1 , k2的两条直线与圆(x﹣x0)2+(y﹣y0)2= ![]() 均相切,且交椭圆于A,B两点.
均相切,且交椭圆于A,B两点.
(1)求证:k1k2=﹣ ![]() ;
;
(2)求|OA||OB|得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) | [15,25 | [25,35 | [35,45 | [45,55 | [55,65 | [65,75 |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据求下面2![]() 2列联表中的
2列联表中的![]() 的值,并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
的值,并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
月收入低于55百元的人数 | 月收入不低于55百元的人数 | 合计 | |
赞成 | a | b | |
不赞成 | c | d | |
合计 | 50 |
(2)若对在[55,65)内的被调查者中随机选取两人进行追踪调查,记选中的2人中不赞成“楼市限购令”的人数为![]() ,求
,求![]() 的概率.
的概率.
附:![]() ,
,![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1的左顶点为A(﹣3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.
=1的左顶点为A(﹣3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A且与圆M相切于点B的直线,交椭圆C于点P,P与椭圆C右焦点的连线交椭圆于Q,若三点B,M,Q共线,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F,C上一点
的焦点F,C上一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A,B两点,若直线AB中点的纵坐标为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com