
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
科目:高中数学 来源: 题型:
【题目】已知直线l:y=k(x+2![]() )与圆O:x2+y2=4相交于不重合的A、B两点,O是坐标原点,且三点A、B、O构成三角形.
)与圆O:x2+y2=4相交于不重合的A、B两点,O是坐标原点,且三点A、B、O构成三角形.
(1)求k的取值范围;
(2)三角形ABO的面积为S,试将S表示成k的函数,并求出它的定义域;
(3)求S的最大值,并求取得最大值时k的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线x2=4y的焦点为F,过点F作斜率为k(k>0)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,过点P作x轴的垂线与抛物线交于点M,若|MF|=4,则直线l的方程为( )
A.![]()
B.y= ![]() x+1
x+1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.函数y=f(x)?g(x)的周期为2
B.函数y=f(x)?g(x)的最大值为1
C.将f(x)的图象向左平移 ![]() 个单位后得到g(x)的图象
个单位后得到g(x)的图象
D.将f(x)的图象向右平移 ![]() 个单位后得到g(x)的图象
个单位后得到g(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雾霾大气严重影响人们的生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为![]() 和
和![]() ,可能的最大亏损率分别为
,可能的最大亏损率分别为![]() 和
和![]() ,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过
,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过![]() 万元.
万元.
![]() Ⅰ
Ⅰ![]() 若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
![]() Ⅱ
Ⅱ![]() 根据
根据![]() 的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx,g(x)= ![]() (m>0).
(m>0).
(1)当m=1时,函数y=f(x)与y=g(x)在x=1处的切线互相垂直,求n的值;
(2)若对任意x>0,恒有|f(x)|≥|g(x)|成立,求实数n的值及实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 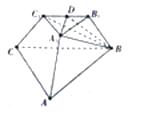
(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间D上的函数f(x)和g(x),如果对任意x∈D,都有|f(x)﹣g(x)|≤1成立,则称f(x)在区间D上可被g(x)替代,D称为“替代区间”.给出以下问题:
①f(x)=x2+1在区间(﹣∞,+∞)上可被g(x)=x2+ ![]() 替代;
替代;
②如果f(x)=lnx在区间[1,e]可被g(x)=x﹣b替代,则﹣2≤b≤2;
③设f(x)=lg(ax2+x)(x∈D1),g(x)=sinx(x∈D1),则存在实数a(a≠0)及区间D1 , D2 , 使得f(x)在区间D1∩D2上被g(x)替代.
其中真命题是( )
A.①②③
B.②③
C.①
D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com