
【题目】如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.

【答案】(1) ![]() .(2) 见解析.
.(2) 见解析.
【解析】(1)解:取CD的中点G,
连结MG,NG.
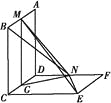
因为四边形ABCD,DCEF为正方形,
且边长为2,
所以MG⊥CD,MG=2,NG=![]() .
.
因为平面ABCD⊥平面DCEF,
所以MG⊥平面DCEF.可得MG⊥NG.
所以MN=![]() =
=![]() .
.
(2)证明:假设直线ME与BN共面,
则AB平面MBEN,且平面MBEN与平面DCEF交于EN.
由题意知两正方形不共面,故AB平面DCEF.
又AB∥CD,所以AB∥平面DCEF,
而EN为平面MBEN与平面DCEF的交线,
所以AB∥EN.
又AB∥CD∥EF,所以EN∥EF,
这与EN∩EF=E矛盾,故假设不成立.
所以ME与BN不共面,它们是异面直线.


科目:高中数学 来源: 题型:
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 中点(图1).将△
中点(图1).将△![]() 沿
沿![]() 折起,使得
折起,使得![]() (图2)在图2中:
(图2)在图2中:
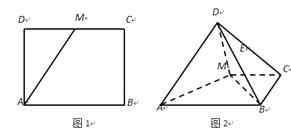
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存点
上是否存点![]() ,使得二面角
,使得二面角![]() 为大小为
为大小为![]() ,说明理由.
,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x),且对任意x>0,都有f′(x)>![]() .
.
(1)判断函数F(x)=![]() 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(3)请将(2)中结论推广到一般形式,并证明你所推广的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(1)求![]() ;
;
(2)除H以外,直线MH与C是否有其它公共点?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-ax-xln x,且f(x)≥0.
(1)求a;
(2)证明:f(x)存在唯一的极大值点x0,且e-2<f(x0)<2-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() ,点
,点![]() 是圆上一动点,
是圆上一动点, ![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com