
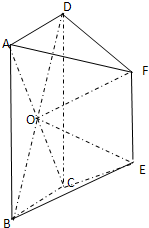
 等腰梯形ABEF中,AB∥EF,AB=
等腰梯形ABEF中,AB∥EF,AB= EF.将此等腰梯形绕其上底边EF所在的直线旋转一定的角度到DCEF位置(如图).
EF.将此等腰梯形绕其上底边EF所在的直线旋转一定的角度到DCEF位置(如图).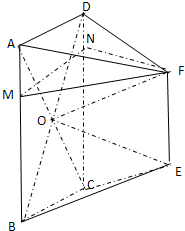 解:(Ⅰ)证明:∵四边形DCEF由四边形ABEF旋转所得,
解:(Ⅰ)证明:∵四边形DCEF由四边形ABEF旋转所得,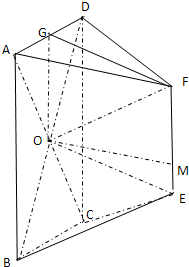
 ,连OM、OG.
,连OM、OG.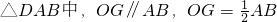 .
.

科目:高中数学 来源: 题型:
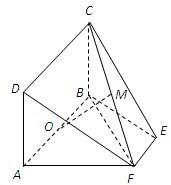 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在的平面和平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在的平面和平面ABEF互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•泉州模拟)等腰梯形ABEF中,AB∥EF,AB=
(2011•泉州模拟)等腰梯形ABEF中,AB∥EF,AB=| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•许昌三模)如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,矩形ABCD所在的平面和平面ABEF互相垂直.
(2011•许昌三模)如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,矩形ABCD所在的平面和平面ABEF互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:
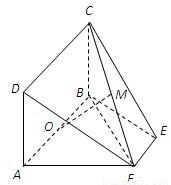
 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1AF⊥BF,O为AB的中点,矩形ABCD所在的平面和平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1AF⊥BF,O为AB的中点,矩形ABCD所在的平面和平面ABEF互相垂直.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳二中等重点中学协作体高考预测数学试卷04(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com