
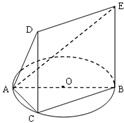
 如图,多面体ABCDE的一个面ABC内接于圆O,AB是圆O的直径,四边形BCDE为平行四边形,且CD⊥平面ABC.
如图,多面体ABCDE的一个面ABC内接于圆O,AB是圆O的直径,四边形BCDE为平行四边形,且CD⊥平面ABC.| 4 | 5 |
| AB2-BC2 |
| BE |
| AB |
| 4 |
| 5 |
| 1 |
| 3 |
| 1 |
| 3 |


科目:高中数学 来源: 题型:

| AK |
| AE |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年东北师大附中、哈师大附中、辽宁实验中学高三第二次模拟考试数学理卷 题型:解答题
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:

(I)求证:平面AEF⊥平面BDG;
(II)若存在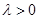 使得
使得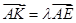 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为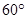 ,求
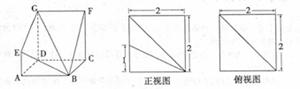
,求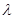 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高二下学期期中考试理数试题 题型:选择题
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在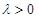 使得
使得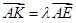 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为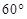 ,求
,求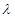 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年东北师大附中、哈师大附中、辽宁实验中学高二第二次考试数学理卷 题型:解答题
(本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;

(II)若存在 使得
使得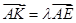 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为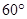 ,求
,求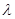 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
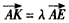 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。 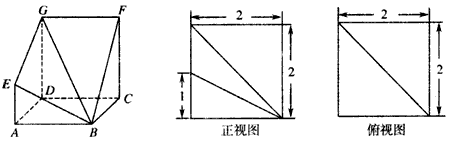
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com