Question

7．已知函数f（x）=$\frac{1}{3}$x³+$\frac{1}{2}$ax²+$\frac{1}{4}$b²x（a，b∈R），若|a-1|+|b-1|≤1，求f′（x）在R上有零点的概率（　　）

• A． $\frac{1}{2}$
• B． $\frac{2}{3}$
• C． $\frac{1}{4}$
• D． $\frac{3}{4}$

Answer 1

分析 首先由题意正确求出使f′（x）在R上有零点的a，b的范围，然后化成可行域，利用面积的关系其概率．

解答 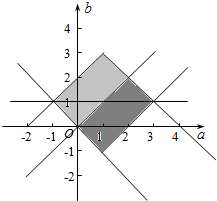解：由题意，f'（x）=（$\frac{1}{3}$x³+$\frac{1}{2}$ax²+$\frac{1}{4}$b²x）'=x²+ax+$\frac{1}{4}{b}^{2}$，要使f′（x）在R上有零点则△=a²-b²≥0，即|a|≥|b|，所以0≤b≤|a|或-|a|≤b＜0，
而|a-1|+|b-1|≤1，对应的区域如图，
由几何概型的概率公式可得f′（x）在R上有零点的概率为$\frac{1}{2}$；
故选：A．

点评 本题主要考查了几何概型，本题先要判断该概率模型，对于几何概型，它的结果要通过长度、面积或体积之比来得到，属于中档题．