
【题目】已知三棱锥P﹣ABC的所有棱长为1.M是底面△ABC内部一个动点(包括边界),且M到三个侧面PAB,PBC,PAC的距离h1,h2,h3成单调递增的等差数列,记PM与AB,BC,AC所成的角分别为α,β,γ,则下列正确的是( )
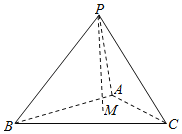
A.α=βB.β=γC.α<βD.β<γ
【答案】D
【解析】
PM与AB,BC,AC所成的角分别为α,β,γ,即比较OM与AB,BC,AC夹角的大小,然后在△ABC中解决问题, 由于d1<d2<d3,可知M在如图阴影区域(不包括边界)
从图中可以看出,OM与BC所成角小于OM与AC所成角,即得解.
依题意知正四面体P﹣ABC的顶点P在底面ABC的射影是正三角形ABC的中心O,
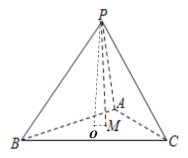
由余弦定理可知,
cosα=cos∠PMOcos<MO,AB>,其中<MO,AB>表示直线MO与AB的夹角,
同理可以将β,γ转化,
cosβ=cos∠PMOcos<MO,BC>,其中<MO,BC>表示直线MO与BC的夹角,
cosγ=cos∠PMOcos<MO,AC>,其中<MO,AC>表示直线MO与AC的夹角,
由于∠PMO是公共的,因此题意即比较OM与AB,BC,AC夹角的大小,
设M到AB,BC,AC的距离为d1,d2,d3 则d1=sin![]() ,其中θ是正四面体相邻两个面所成角,sinθ
,其中θ是正四面体相邻两个面所成角,sinθ![]() ,
,
所以d1,d2,d3成单调递增的等差数列,然后在△ABC中解决问题
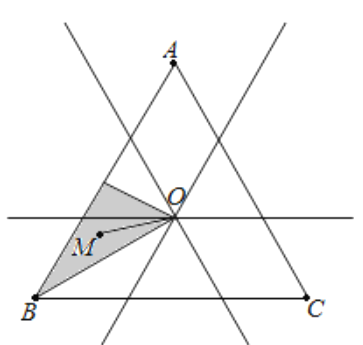
由于d1<d2<d3,可知M在如图阴影区域(不包括边界)
从图中可以看出,OM与BC所成角小于OM与AC所成角,所以β<γ,
故选:D.


科目:高中数学 来源: 题型:
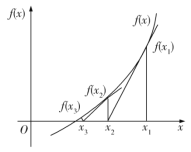
【题目】牛顿迭代法(Newton's method)又称牛顿–拉夫逊方法(Newton–Raphsonmethod),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设![]() 是
是![]() 的根,选取
的根,选取![]() 作为
作为![]() 初始近似值,过点
初始近似值,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 与
与![]() 轴的交点的横坐标
轴的交点的横坐标![]() ,称
,称![]() 是
是![]() 的一次近似值,过点
的一次近似值,过点![]() 作曲线
作曲线![]() 的切线,则该切线与
的切线,则该切线与![]() 轴的交点的横坐标为
轴的交点的横坐标为![]() ,称
,称![]() 是
是![]() 的二次近似值.重复以上过程,直到
的二次近似值.重复以上过程,直到![]() 的近似值足够小,即把
的近似值足够小,即把![]() 作为
作为![]() 的近似解.设
的近似解.设![]() 构成数列
构成数列![]() .对于下列结论:
.对于下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,离心率为
中,离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 两点.若直线
两点.若直线![]() 斜率为
斜率为 ![]() 时,
时, ![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试问以![]() 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线![]() 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线Γ:y2=2px(p>0)的焦点为F,P是抛物线Γ上一点,且在第一象限,满足![]() (2,2
(2,2![]() )
)
(1)求抛物线Γ的方程;
(2)已知经过点A(3,﹣2)的直线交抛物线Γ于M,N两点,经过定点B(3,﹣6)和M的直线与抛物线Γ交于另一点L,问直线NL是否恒过定点,如果过定点,求出该定点,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大约在20世纪30年代,世界上许多国家都流传着这样一个题目:任取一个正整数![]() ,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取
,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取![]() ,则要想算出结果1,共需要经过的运算步数是( )
,则要想算出结果1,共需要经过的运算步数是( )
A.9B.10C.11D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn+1﹣bn=![]() (n∈N+)且b1=3,求数列
(n∈N+)且b1=3,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 的动圆恒与
的动圆恒与![]() 轴相切,
轴相切,![]() 为该圆的直径,设点
为该圆的直径,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的任意直线
的任意直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,
,![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,除
,除![]() 以外,直线
以外,直线![]() 与
与![]() 是否有其它公共点?说明理由.
是否有其它公共点?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com