
【题目】在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
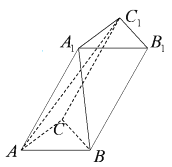
连结A1C,交AC1于点E,取BC的中点D,连结AD、DE.证出DE是△A1BC的中位线,得DE![]() A1B,因此AE、ED所成的锐角或直角就是A1B与AC1所成的角.然后利用题中数据在△AED中分别算出边AE、ED、AD的长,根据余弦定理列式,即可算出异面直线A1B与AC1所成角的余弦值.
A1B,因此AE、ED所成的锐角或直角就是A1B与AC1所成的角.然后利用题中数据在△AED中分别算出边AE、ED、AD的长,根据余弦定理列式,即可算出异面直线A1B与AC1所成角的余弦值.
连结A1C,交AC1于点E,取BC的中点D,连结AD、DE,
∵四边形AA1C1C是平行四边形,∴E是A1C的中点
∵D是BC的中点,∴DE是△A1BC的中位线,可得DE![]() A1B,
A1B,
因此,∠AED(或其补角)就是异面直线A1B与AC1所成的角.
设AB=AC=![]() AA1=2,∵∠A1AB=60°,可得A1B=
AA1=2,∵∠A1AB=60°,可得A1B=![]() ,且∠A1BA=90°
,且∠A1BA=90°
∴△A1BA是直角三角形,得DE![]() A1B=
A1B=![]() .
.
同理,直角△A1CA中, AE![]() ,
,
又∵∠BAC=90°,AB=AC=2,D为BC中点,
∴AD![]() BC
BC![]()
由此可得△ADE中,cos∠AED![]() .
.
即异面直线A1B与AC1所成角的余弦值为![]() .
.
故选:C.


科目:高中数学 来源: 题型:
【题目】某校寒假行政值班安排,要求每天安排一名行政人员值日,现从包含甲、乙两人的七名行政人员中选四人负责四天的轮班值日,在下列条件下,各有多少种不同的安排方法?
(1)甲、乙两人都被选中,且安排在前两天值日;
(2)甲、乙两人只有一人被选中,且不能安排在后两天值日.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本![]() 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为![]() 元.
元.
(Ⅰ)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数(利润=总售价-成本-促销费);
万元的函数(利润=总售价-成本-促销费);
(Ⅱ)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①相关指数![]() 越小,则残差平方和越小,模型的拟合效果越好.
越小,则残差平方和越小,模型的拟合效果越好.
②在![]() 的列联表中我们可以通过等高条形图直观判断两个变量是否有关.
的列联表中我们可以通过等高条形图直观判断两个变量是否有关.
③残差点比较均匀地落在水平带状区域内,带状区域越窄,说明模型拟合精度越高.
④两个随机变量相关性越强,则相关系数r越接近1.
其中正确命题的个数为( ).
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生![]() 人,学校团委为了了解本校学生到上述红色基地硏学旅行的情况,随机调查了
人,学校团委为了了解本校学生到上述红色基地硏学旅行的情况,随机调查了![]() 名学生,其中到过中共一大会址或井冈山研学旅行的共有
名学生,其中到过中共一大会址或井冈山研学旅行的共有![]() 人,到过井冈山研学旅行的
人,到过井冈山研学旅行的![]() 人,到过中共一大会址并且到过井冈山研学旅行的恰有
人,到过中共一大会址并且到过井冈山研学旅行的恰有![]() 人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有( )人
人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有( )人
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com