证明:(1)由f(2-x)=f(x)知,函数f(x)图象关于直线x=1对称,
则根据②可知:对于x,y∈[0,1],若x+y≤1,
则f(x+y)≥f(x)+f(y)-1.…
(2)设x
1,x
2∈[0,1],且x
1<x
2,则x
2-x
1∈[0,1].
∵f(x
2)-f(x
1)=f[x
1+(x
2-x
1)]-f(x
1)≥f(x
1)+f(x
2-x
1)-1-f(x
1)=f(x
2-x
1)-1≥0,
∴f(x)在[0,1]上是不减函数.…
∵

,
∴

=

.…
(3)对于任意x∈(0,1],则必存在正整数n,使得

.
因为f(x)在(0,1)上是不减函数,所以

,
由(2)知

.
由①可得f(2)≥1,在②中,令x=y=2,得f(2)≤1,∴f(2)=1.
而f(2)=f(0),∴f(0)=1,又

,∴

,
∴x∈[0,1]时,1≤f(x)≤6x+1..…
∵x∈[1,2]时,2-x∈[0,1],且f(x)=f(2-x),
∴1≤f(2-x)≤6(2-x)+1=13-6x,
因此,x∈[1,2]时,1≤f(x)≤13-6x.….
分析:(1)由f(2-x)=f(x)知,函数f(x)图象关于直线x=1对称,则根据②可知:对于x,y∈[0,1],若x+y≤1,
两者结合即得;
(2)先利用单调函数的定义证明f(x)在[0,1]上是不减函数,利用

,进行放缩结合等比数列的求和即得;(3)对于任意x∈(0,1],则必存在正整数n,使得

.因为f(x)在(0,1)上是不减函数,所以

,由(2)知

,结合题中条件充分利用赋值法及不等式的性质即可.
点评:本题主要考查函数单调性的性质、函数单调性的判断与证明、数列知识与函数知识的综合问题.解答关键在于对赋值法的熟练应用.

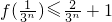 (n∈N*);
(n∈N*); ,
,
 .…
.… .
. ,
, .
. ,∴
,∴ ,
, ,进行放缩结合等比数列的求和即得;(3)对于任意x∈(0,1],则必存在正整数n,使得
,进行放缩结合等比数列的求和即得;(3)对于任意x∈(0,1],则必存在正整数n,使得 .因为f(x)在(0,1)上是不减函数,所以
.因为f(x)在(0,1)上是不减函数,所以 ,由(2)知
,由(2)知 ,结合题中条件充分利用赋值法及不等式的性质即可.
,结合题中条件充分利用赋值法及不等式的性质即可.
