
【题目】若函数f(x)=x3﹣ ![]() x2+bx+c在x=1时取得极值,且当x∈[﹣1,2]时,f(x)<c2恒成立.
x2+bx+c在x=1时取得极值,且当x∈[﹣1,2]时,f(x)<c2恒成立.
(1)求实数b的值;
(2)求实数c的取值范围.
【答案】
(1)解:∵f(x)=x3﹣ ![]() x2+bx+c,
x2+bx+c,
∴f′(x)=3x2﹣x+b,
∵x=1是方程3x2﹣x+b=0的一个根,
设另一个根是x0,则 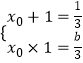 ,
,
∴x0=﹣ ![]() ,b=﹣2
,b=﹣2
(2)解:由(1)知,f(x)=x3﹣ ![]() x2﹣2x+c,
x2﹣2x+c,
∴f′(x)=3x2﹣x﹣2=(3x+2)(x﹣1),
令f′(x)=0,解得x1=﹣ ![]() ,x2=1;
,x2=1;
列表如下:
x | [﹣1,﹣ | ﹣ | (﹣ | 1 | (1,2] |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
由表格知,f(x)取得极大值f(﹣ ![]() )=
)= ![]() +c,
+c,
又f(2)=2+c,
∴当x=2时,函数取得最大值f(x)max=2+c;
∴2+c<c2,
解得c<﹣1或c>2,
∴c的取值范围是(﹣∞,﹣1)∪(2,+∞)
【解析】(1)求出f(x)的导数f′(x),由函数的零点以及根与系数的关系求出b的值;(2)利用导数求出f(x)在闭区间[﹣1,2]上的最大值f(x)max , 令其小于c2 , 求出c的取值范围.
【考点精析】利用函数的极值与导数和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() (x>0,m>0)和函数g(x)=a|x﹣b|+c(x∈R,a>0,b>0).问:
(x>0,m>0)和函数g(x)=a|x﹣b|+c(x∈R,a>0,b>0).问:
(1)证明:f(x)在( ![]() ,+∞)上是增函数;
,+∞)上是增函数;
(2)把函数g1(x)=|x|和g2(x)=|x﹣1|写成分段函数的形式,并画出它们的图象,总结出g2(x)的图象是如何由g1(x)的图象得到的.请利用上面你的结论说明:g(x)的图象关于x=b对称;
(3)当m=1,b=2,c=0时,若f(x)>g(x)对于任意的x>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x+1|<1},B={x|y= ![]() ,y∈R},则A∩RB=( )
,y∈R},则A∩RB=( )
A.(﹣2,1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(0)=2和f(x+1)﹣f(x)=2x﹣1对任意实数x都成立.
(1)求函数f(x)的解析式;
(2)当t∈[﹣1,3]时,求y=f(2t)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com