Question

已知f(x)=x(x-a)(x-b)，点A(s，f(s))，B(t，f(t))．

(Ⅰ)若a=b=1，求函数f(x)的单调递增区间；

(Ⅱ)若函数f(x)的导函数f′(x)满足：当|x|≤1时，有|f′(x)|≤恒成立，求函数f(x)的解析表达式；

(Ⅲ)若0＜a＜b，函数f(x)在x=s和x=t处取得极值，且a+b=，证明：与不可能垂直.

Answer 1

答案：解：(Ⅰ)f(x)=x³-2x²+x，

f′(x)=3x²-4x+1

令f′(x)≥0得3x²-4x+1≥0，

解得x≤或x≥1，

故f(x)的增区间(-∞，]和[1，+∞) 

(Ⅱ)f′(x)=3x²-2(a+b)x+ab

当x∈[-1，1)时，恒有|f′(x)|≤．

故有≤f′(1)≤，≤f′(-1)≤，

及≤f′(0)≤，

即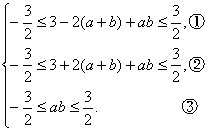

①+②，得≤ab≤，

又由③，得ab=，将上式代回①和②，

得a+b=0，

故f(x)=x³-x． 

(Ⅲ)假设⊥，

即·=(s，f(x))·(t，f(t))=st+f(s)f(t)=0

故(s-a)(s-b)(t-a)(t-b)=-1，

[st-(s+t)a+a²][st-(s+t)b+b²]=-1，

由s，t为f′(x)=0的两根可得，

s+t=(a+b)，st=，(0＜a＜b)

从而有ab(a-b)²=9．

这样(a+b)²=(a-b)²+4ab

=

即a+b≥，这与a+b＜矛盾．

故与不可能垂直．