
分析 先求出f(-12)=1+ln($\sqrt{170}+13$),f(14)=1+ln($\sqrt{170}-13$),由此利用对数性质能求出f(-12)+f(14)的值.
解答 解:∵$f(x)=1+ln({\sqrt{{x^2}-2x+2}-x+1})$,
∴f(-12)=1+ln($\sqrt{144+24+2}$+12+1)=1+ln($\sqrt{170}+13$),
f(14)=1+ln($\sqrt{196-28+2}$-14+1)=1+ln($\sqrt{170}-13$),
∴f(-12)+f(14)=2+[ln($\sqrt{170}+13$)+ln($\sqrt{170}$-13)]=2+ln1=2.
故答案为:2.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
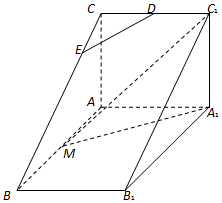 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p为真命题,q为假命题 | B. | p为假命题,q为假命题 | ||
| C. | p为真命题,q为真命题 | D. | p为假命题,q为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
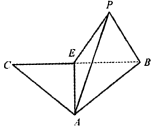 等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.
等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80 | B. | 100 | C. | 120 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com