
【题目】小明一家订阅的晚报会在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
【答案】(1) 事件A发生的可能性大(2)![]()
【解析】试题分析:设晚报被送到的时间为下午x时,小明家晚餐开始的时间为下午y时,(x,y)可以看成平面中的点,试验的全部结果所构成的区域为Ω={(x,y)|5.5≤x≤6.5,6≤y≤7}一个正方形区域,求出其面积,事件A表示小明晚餐前不能被送到,所构成的区域为A={(X,Y)|5.5≤x≤6.5,6≤y≤7,x<y} 求出其面积,根据几何概型的概率公式解之即可.
解析:建立如图所示的坐标系.
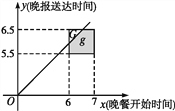
图中直线x=6,x=7,y=5.5,y=6.5围成一个正方形区域G,该试验的所有结果与区域G内的点(x,y)一一对应.由题意知,每次结果出现的可能性是相同的,是几何概型.
(1)作射线y=x(x>0).晚报在晚餐前送达即y<x,因此图中阴影部分表示事件A:“晚报在晚餐前送达”.而G中空白部分则表示事件B:“晚报在晚餐开始后送到”.由图知事件A发生的可能性大.
(2)易求G的面积为1,而g的面积为![]() ,由几何概型的概率公式可得P(A)=
,由几何概型的概率公式可得P(A)=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若不等式
时,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若方程
时,若方程![]() 在
在![]() 上总有两个不等的实根, 求
上总有两个不等的实根, 求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣1:平面几何
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
(1)求证:∠DEA=∠DFA;
(2)若∠EBA=30°,EF= ![]() ,EA=2AC,求AF的长.
,EA=2AC,求AF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20,30) | 30 | 18 |
[30,40) | 36 | 24 |
[40,50) | 12 | 9 |
[50,60] | 4 | 3 |
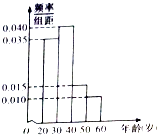
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com