
已知![]() ,且
,且![]()
1.设![]() ,求
,求![]() 的解析式;
的解析式;
2.设![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使
,使![]() 在
在![]() 内为减函数,且在(-1,0)内是增函数.
内为减函数,且在(-1,0)内是增函数.
1.由题意得![]() ,
,
![]() ,
,
∴![]()
∴![]()
2.![]() .
.
若满足条件的![]() 存在,则
存在,则![]()
∵函数![]() 在
在![]() 内是减函数,∴当
内是减函数,∴当![]() 时,
时,![]() ,
,
即![]() 对于
对于![]() 恒成立.
恒成立.
∴![]()
∴![]() ,解得
,解得![]() .
.
又函数![]() 在(-1,0)上是增函数,∴当
在(-1,0)上是增函数,∴当![]() 时,
时,![]()
即![]() 对于
对于![]() 恒成立,
恒成立,
∴![]()
∴![]() ,解得
,解得![]() .
.
故当![]() 时,
时,![]() 在
在![]() 上是减函数,在(-1,0)上是增函数,即满足条件的
上是减函数,在(-1,0)上是增函数,即满足条件的![]() 存在.
存在.
根据题设条件可以求出![]() 的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数
的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数![]() 是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数
是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数![]() 的取值范围,使问题获解.
的取值范围,使问题获解.


科目:高中数学 来源:2011-2012学年河北省高三第三次月考文科数学试卷 题型:解答题
已知函数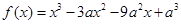 .
.
(1)设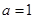 ,求函数
,求函数 的极值;
的极值;
(2)若 ,且当
,且当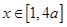 时,
时,
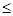 12a恒成立,试确定
12a恒成立,试确定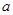 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:山东省聊城一中2010届高三上学期模块测试(理) 题型:解答题
已知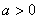 ,且
,且 ≠1,设
≠1,设 函数
函数 在
在 内单调递减;q:函数
内单调递减;q:函数
 有两个不同零点点,如果
有两个不同零点点,如果 和
和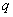 有且只有一个正确,求
有且只有一个正确,求 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com