
【题目】已知f(x)=e2x﹣x2﹣a.
(1)证明f(x)在(﹣∞,+∞)上为增函数;
(2)当a=1时,解不等式f[f(x)]>x;
(3)若f[f(x)﹣x2﹣2x]>f(x)在(0,+∞)上恒成立,求a的最大整数值.
【答案】
(1)证明:f'(x)=2e2x﹣2x=2(e2x﹣x),
设g(x)=e2x﹣x,g'(x)=2e2x﹣1=0, ![]() ,
, ![]() ,
,
x,g′(x),g(x)的变化如下:
x | (﹣∞, |
| ( |
g′(x) | ﹣ | 0 | + |
g(x) | ↓ | 极小值 | ↑ |
∴ ![]() =
= ![]() ,
,
∴g(x)>0,∴f'(x)>0,∴f(x)在R上为增函数
(2)解:a=1时,f(x)=e2x﹣x2﹣1,
∵f(x)在R上为增函数,∴若f(x)≤x,
则f[f(x)]≤f(x)≤x,与f[f(x)]>x矛盾;
若f(x)>x,则f[f(x)]>f(x)>x,故成立.
经化简f[f(x)]>x,则f(x)>x,∴e2x﹣x2﹣1>x,即e2x>x2+x+1,
∵x2+x+1>0,即2x>ln(x2+x+1),
∴设h(x)=2x﹣ln(x2+x+1),
h′(x)=2﹣ ![]() =
= ![]() >0,
>0,
∴h(x)在R上为增函数,∴h(x)>h(0),得x>0,
∴原不等式解集为(0,+∞)
(3)解:∵f(x)在R上为增函数,∴f(x)﹣x2﹣2x>x,即e2x﹣2x2﹣3x>a,
令G(x)=e2x﹣2x2﹣3x,G′(x)=2e2x﹣4x﹣3=2(e2x﹣2x﹣ ![]() ),
),
设H(x)=e2x﹣2x﹣ ![]() ,H′(x)=2e2x﹣2,
,H′(x)=2e2x﹣2,
∴x>0时,e2x>1,H′(x)>0,
∴H(x)在(0,+∞)为增函数,
∴G′(x)=2H(x)在(0,+∞)为增函数,
G′( ![]() )=2(e﹣
)=2(e﹣ ![]() )>0,G′(
)>0,G′( ![]() )=2(
)=2( ![]() ﹣
﹣ ![]() )<0,
)<0,
∴G'(x)=0有任一解,设为x0∈( ![]() ,
, ![]() ),
),
∴x>0时,x,G′(x),G(x)的变化如下:
x | (0,x0) | x0 | (x0,+∞) |
G′(x) | ﹣ | 0 | + |
G(x) | ↓ | 极小值 | ↑ |
∴G(x)min=G(x0)= ![]() ﹣2
﹣2 ![]() ﹣3x0,
﹣3x0,
∵ ![]() ﹣2x0﹣
﹣2x0﹣ ![]() =0,即
=0,即 ![]() =2x0+
=2x0+ ![]() ,
,
∴G(x)min=﹣2 ![]() ﹣x0+
﹣x0+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
又∵a∈Z,∴amax=0
【解析】(1)求出函数的导数,求出导函数的导数,求出导函数的单调区间,从而证明函数的单调性即可;(2)求出函数的解析式,问题转化为e2x>x2+x+1,由x2+x+1>0,得2x>ln(x2+x+1),设h(x)=2x﹣ln(x2+x+1),根据函数的单调性求出不等式的解集即可;(3)令G(x)=e2x﹣2x2﹣3x,求出函数的导数,设H(x)=e2x﹣2x﹣ ![]() ,根据函数的单调性求出G(x)的最小值,从而求出a的最大值即可.
,根据函数的单调性求出G(x)的最小值,从而求出a的最大值即可.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,AB=AC=CC1 , 平面BAC1⊥平面ACC1A1 , ∠ACC1=∠BAC1=60°,AC1∩A1C=O. 
(Ⅰ)求证:BO⊥平面AA1C1C;
(Ⅱ)求二面角A﹣BC1﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD中,AB=BD=AD=2,BC=1,CD= ![]() ,若二面角A﹣BD﹣C的取值范围为[
,若二面角A﹣BD﹣C的取值范围为[ ![]() ,
, ![]() ],则该几何体的外接球表面积的取值范围为 .
],则该几何体的外接球表面积的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx(x>0).
(Ⅰ)求证:f(x)≥1﹣ ![]() ;
;
(Ⅱ)设g(x)=x2f(x),且关于x的方程x2f(x)=m有两个不等的实根x1 , x2(x1<x2).
(i)求实数m的取值范围;
(ii)求证:x1x22< ![]() .
.
(参考数据:e=2.718, ![]() ≈0.960,
≈0.960, ![]() ≈1.124,
≈1.124, ![]() ≈0.769,ln2≈0.693,ln2.6≈0.956,ln2.639≈0.970.注:不同的方法可能会选取不同的数据)
≈0.769,ln2≈0.693,ln2.6≈0.956,ln2.639≈0.970.注:不同的方法可能会选取不同的数据)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(2x﹣3)﹣ax2+2ax+b,若函数 f(x)存在两个极值点x1 , x2 , 且极小值点x1大于极大值点x2 , 则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() ,离心率
,离心率 ![]() ,它的长轴长等于圆x2+y2﹣2x+4y﹣3=0的直径.
,它的长轴长等于圆x2+y2﹣2x+4y﹣3=0的直径.
(1)求椭圆 C的方程;
(2)若过点 ![]() 的直线l交椭圆C于A,B两点,是否存在定点Q,使得以AB为直径的圆经过这个定点,若存在,求出定点Q的坐标;若不存在,请说明理由?
的直线l交椭圆C于A,B两点,是否存在定点Q,使得以AB为直径的圆经过这个定点,若存在,求出定点Q的坐标;若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.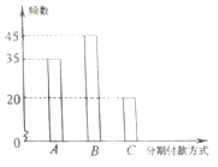
(1)求甲乙两人采用不同分期付款方式的概率;
(2)记X(单位:万元)为该汽车经销商从甲乙两人购车中所获得的利润,求X的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com