
【题目】三棱锥ABCD中,BC=DC=AB=AD= ![]() ,BD=2,平面ABD⊥平面BCD,O为BD的中点,P、Q分别为线段AO,BC上的动点,且AP=CQ,求三棱锥PQCO体积的最大值.
,BD=2,平面ABD⊥平面BCD,O为BD的中点,P、Q分别为线段AO,BC上的动点,且AP=CQ,求三棱锥PQCO体积的最大值.
科目:高中数学 来源: 题型:
【题目】关于实数x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},则关于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系: f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(Ⅰ)求实验室这一天的最大温差;
(Ⅱ)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):
月收入(百元) | 赞成人数 |
[15,25) | 8 |
[25,35) | 7 |
[35,45) | 10 |
[45,55) | 6 |
[55,65) | 2 |
[65,75) | 2 |
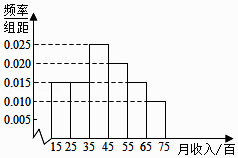
(Ⅰ)试根据频率分布直方图估计这60人的中位数和平均月收入;
(Ⅱ)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求被选取的2人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.
(1)求AC边所在直线方程;
(2)求顶点C的坐标;
(3)求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题P:实数x满足2x2﹣5ax﹣3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=2,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( ) 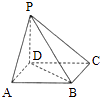
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com