
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)求函数![]() 与
与![]() 的解析式,并求出
的解析式,并求出![]() ,
,![]() 的定义域;
的定义域;
(2)设![]() ,试求函数
,试求函数![]() 的定义域,及最值.
的定义域,及最值.
【答案】(1)f(x)=log3(x+2)﹣1,定义域[﹣1,7];g(x)=log3x+2,定义域[1,9];(2)定义域[1,3],最小值6,最大值13.
【解析】
(1)令t=3x﹣2,则x=log3(t+2)﹣1,根据已知可求f(x),进而可求g(x);
(2)结合(1)可求h(x),然后结合函数的定义域的要求有![]() ,解出x的范围,结合二次函数的性质可求.
,解出x的范围,结合二次函数的性质可求.
(1)令t=3x﹣2,则x=log3(t+2)﹣1,∵x∈[0,2],∴t∈[﹣1,8],
∵f(3x﹣2)=x﹣1(x∈[0,2]),∴f(t)=log3(t+2)﹣1,t∈[﹣1,7],
∴f(x)=log3(x+2)﹣1,x∈[﹣1,7],即f(x)的定义域[﹣1,7],
∵g(x)=f(x﹣2)+3=log3x+2,∴x﹣2∈[﹣1,7],∴x∈[1,9],即g(x)的定义域[1,9].
(2)∵h(x)=[g(x)]2+g(x2)=(log3x+2)2+2![]() 6log3x+6,
6log3x+6,
∵![]() ,∴1≤x≤3,即函数y=h(x)的定义域[1,3],∵0≤log3x≤1,
,∴1≤x≤3,即函数y=h(x)的定义域[1,3],∵0≤log3x≤1,
结合二次函数的性质可知,当log3x=0时,函数取得最小值6,
当log3x=1时,函数取得最大值13.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为![]() (
(![]() 为常数)元,之后每年会投入一笔研发资金,
为常数)元,之后每年会投入一笔研发资金,![]() 年后总投入资金记为
年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() 为常数,
为常数,![]() .已知
.已知![]() 年后总投入资金为研发启动时投入资金的
年后总投入资金为研发启动时投入资金的![]() 倍.问
倍.问
(1)研发启动多少年后,总投入资金是研发启动时投入资金的![]() 倍;
倍;
(2)研发启动后第几年的投入资金的最多.
查看答案和解析>>
科目:高中数学 来源: 题型:
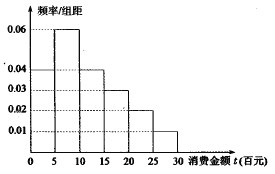
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
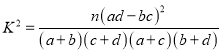 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,并且图象关于y轴对称,当x≤-1时,y=f(x)的图象是经过点(-2,0)与(-1,1)的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(1,1)的一段抛物线.
(1)试求出函数f(x)的表达式,作出其图象;
(2)根据图象说出函数的单调区间,以及在每一个单调区间上函数是增函数还是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点 ,且两个焦点的坐标分别为
,且两个焦点的坐标分别为![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 上的三个不同的点,
上的三个不同的点, ![]() 为坐标原点,且
为坐标原点,且![]() ,求证:四边形
,求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
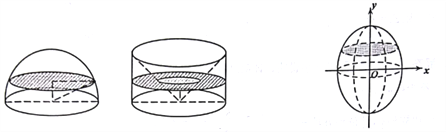
【题目】我国南北朝时间著名数学家祖暅提出了祖暅原理:“幂势既同,则积不容异”.意思是:夹在两平行平面间的两个几何体,被平行于这两个平行平面的任何平面所载,若截得的两个截面面积总相等,则这两个几何体的体积相等.为计算球的体积,构造一个底面半径和高都与球半径相等的圆柱,然后再圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,运用祖暅原理可证明此几何体与半球体积相等(任何一个平面所载的两个截面面积都相等).将椭圆![]() 绕
绕![]() 轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com