若函数f(x)=x2-2|x|
(1)判断函数在(-∞,∞)的奇偶性,并画出函数的图象;
(2)求方程f(x)+a=0有两实数解的a的取值范围.
解:(1)函数的定义域为R,f(-x)=x
2-2|x|=f(x),所以函数是偶函数
当x≥0时,f(x)=x
2-2x=(x-1)
2-1,
函数的图象如图
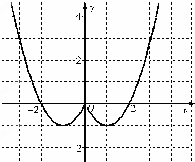
(2)方程f(x)+a=0有两实数解,即y=f(x)与y=-a有两个不同的交点
由图象可知-a>0
所以a<0.
分析:(1)确定函数的定义域,验证f(-x)与f(x)的关系,可得函数的奇偶性;利用配方法确定函数的对称轴与顶点坐标,即可得到函数的图象;
(2)方程f(x)+a=0有两实数解,即y=f(x)与y=-a有两个不同的交点,由图象可知结论.
点评:本题考查函数图象的作法,考查函数的奇偶性,考查利用图象确定方程的解,属于中档题.
