
【题目】已知函数![]() .
.
(1)证明:![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值和
的最大值和![]() 的最小值.
的最小值.
【答案】(1)证明见解析(2)![]() 的最大值为
的最大值为![]() ,
,![]() 的最小值为1
的最小值为1
【解析】
(1)当![]() 时,对函数进行求导,利用导数可以求出函数的最小值,利用奇偶性再进行判断即可;
时,对函数进行求导,利用导数可以求出函数的最小值,利用奇偶性再进行判断即可;
(2)化简![]() ,不等式可以转化为:
,不等式可以转化为:![]() ,
,![]() ,令
,令![]() ,求导,根据
,求导,根据![]() 的不同取值,判断出函数的单调性,最后分类讨论进行求解即可.
的不同取值,判断出函数的单调性,最后分类讨论进行求解即可.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
则当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,![]() ,
,
又函数![]() 为偶函数,则对任意
为偶函数,则对任意![]() ,
,![]() 成立,
成立,
(2)![]() ,
,
当![]() 时,
时,![]() ,即为
,即为![]() ,
,
![]() ,即为
,即为![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,![]() ;
;
当![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,![]() ;
;
当![]() 时,存在唯一的
时,存在唯一的![]() ,使得
,使得![]() ,
,
![]() 与
与![]() 在区间
在区间![]() 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| 增 | 极大值 | 减 |
![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() ,
,
进一步,当![]() 时
时![]() ,当且仅当
,当且仅当![]() ,
,
可得![]() .
.
综上所述,当且仅当![]() 时,
时,![]() 在
在![]() 上恒成立;
上恒成立;
当且仅当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 的最大值为
的最大值为![]() ,
,![]() 的最小值为1.
的最小值为1.


科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:
对于任意![]() ,都有
,都有![]() 成立.
成立.
①求数列![]() 的通项公式;
的通项公式;
②设数列![]() ,问:数列
,问:数列![]() 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和![]() 列联表:
列联表:
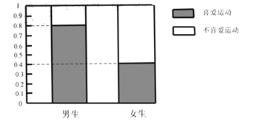
喜爱运动 | 不喜爱运动 | 总计 | |
男生 |
|
| 30 |
女生 |
|
| 20 |
总计 | 50 |
(1)求出列联表中![]()
![]()
![]()
![]() 的值;
的值;
(2)是否有![]() 的把握认为喜爱运动与性别有关?附:参考公式和数据:
的把握认为喜爱运动与性别有关?附:参考公式和数据: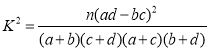 ,(其中
,(其中![]() )
)
0.500 | 0.100 | 0.050 | 0.010 | 0.001 | |
| 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年安庆市在大力推进城市环境、人文精神建设的过程中,居民生活垃圾分类逐渐形成意识.有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识"的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图:
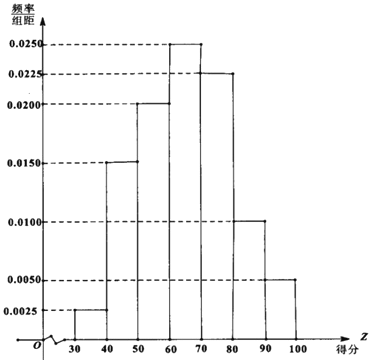
(1)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(
近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(![]() );
);
(2)在(1)的条件下,有关部门为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 可获赠2次随机话费,得分低于
可获赠2次随机话费,得分低于![]() 则只有1次:
则只有1次:
(ii)每次赠送的随机话费和对应概率如下:
赠送话费(单位:元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加问卷调查获赠的话费,求X的分布列.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的焦距为
的焦距为![]() ,斜率为
,斜率为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过左焦点![]() 斜率为
斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]()
![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,问:
,问:![]() 是否为定值?若是,求出此定值,若不是,说明理由.
是否为定值?若是,求出此定值,若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com