
【题目】如图,扇形AOB是一个观光区的平面示意图,其中圆心角∠AOB为![]() ,半径OA为1 km.为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段DB组成,其中D在线段OB上,且CD∥AO.设∠AOC=θ.
,半径OA为1 km.为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段DB组成,其中D在线段OB上,且CD∥AO.设∠AOC=θ.
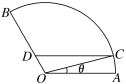
(1)用θ表示CD的长度,并写出θ的取值范围;
(2)当θ为何值时,观光道路最长?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用![]() 表示CD的长度的关键是在
表示CD的长度的关键是在![]() 中正确利用正弦定理;
中正确利用正弦定理;
(2)首先将道路长度![]() 表达成
表达成![]() 的函数关系式,再利用导数方法研究函数的最大值,从而可以求得
的函数关系式,再利用导数方法研究函数的最大值,从而可以求得![]() 时,观光道路最长.
时,观光道路最长.
(1)在△OCD中,由正弦定理,得
![]() =
=![]() =
=![]() =
=![]() ,
,
所以CD=![]() sin
sin![]() =cos θ+
=cos θ+![]() sin θ,OD=
sin θ,OD=![]() sin θ,
sin θ,
因为OD<OB,即![]() sin θ<1,所以sin θ<
sin θ<1,所以sin θ<![]() ,所以0<θ<
,所以0<θ<![]() ,
,
所以CD=cos θ+![]() sin θ,θ的取值范围为
sin θ,θ的取值范围为![]() .
.
(2)设观光道路长度为L(θ),
则L(θ)=BD+CD+弧CA的长
=1-![]() sin θ+cos θ+
sin θ+cos θ+![]() sin θ+θ
sin θ+θ
=cos θ-![]() sin θ+θ+1,θ∈
sin θ+θ+1,θ∈![]() ,
,
L′(θ)=-sin θ-![]() cos θ+1,
cos θ+1,
由L′(θ)=0,得sin![]() =
=![]() ,
,
又θ∈![]() ,所以θ=
,所以θ=![]() ,
,
列表:
θ |
|
|
|
L′(θ) | + | 0 | - |
L(θ) | 增函数 | 极大值 | 减函数 |
所以当θ=![]() 时,L(θ)达到最大值,即当θ=
时,L(θ)达到最大值,即当θ=![]() 时,观光道路最长.
时,观光道路最长.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
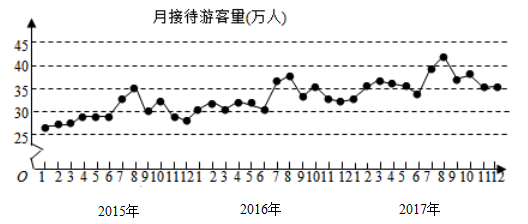
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1.

(1)求证:AB1⊥平面A1BC1;
(2)若D在B1C1上,满足B1D=2DC1,求AD与平面A1BC1所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且△PF1F2的面积为2.
,且△PF1F2的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为1的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于A,B两点,与椭圆C交于C,D两点,且
的圆交于A,B两点,与椭圆C交于C,D两点,且![]() (
(![]() ),当
),当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布表,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布表,其中![]() .(计算结果保留两位小数)
.(计算结果保留两位小数)
分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频率 | 0.08 |
| 0.35 | 0.27 |
|
(1)试估计被调查的员工的满意程度的中位数;
(2)若把每组的组中值作为该组的满意程度,试估计被调查的员工的满意程度的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,函数
,函数![]() 与
与![]() 关于直线
关于直线![]() 对称.
对称.
(1)若函数![]() 在区间
在区间![]() 上递增,求a的取值范围;
上递增,求a的取值范围;
(2)证明:![]() ;
;
(3)设![]() ,其中
,其中![]() 恒成立,求满足条件的最小正整数b的值.
恒成立,求满足条件的最小正整数b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 的中点为
的中点为![]() ,
,![]() ,
,![]() 两点为曲线
两点为曲线![]() 上关于原点
上关于原点![]() 对称的两点,且
对称的两点,且![]() (
(![]() ),求四边形
),求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com