
【题目】已知函数![]() ,直线
,直线![]() 与
与![]() 的图象的相邻两个交点的横坐标分别是
的图象的相邻两个交点的横坐标分别是![]() 和
和![]() ,现有如下命题:
,现有如下命题:
①该函数在![]() 上的值域是
上的值域是![]() ;
;
②在![]() 上,当且仅当
上,当且仅当![]() 时函数取最大值;
时函数取最大值;
③该函数的最小正周期可以是![]() ;
;
④![]() 的图象可能过原点.
的图象可能过原点.
其中的真命题有__________.(写出所有真命题的序号)
【答案】④
【解析】当![]() 时,区间
时,区间![]() 没有意义,故①错误;该函数在
没有意义,故①错误;该函数在![]() 上,当
上,当![]() 时函数取最小值,故②错误;由周期公式
时函数取最小值,故②错误;由周期公式![]() ,得
,得![]() ,此时
,此时![]() ,由
,由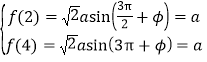 ,计算得出
,计算得出![]() ,不满足
,不满足![]() ,可以知道该函数的最小正周期不可以是
,可以知道该函数的最小正周期不可以是![]() ,故③错误;由
,故③错误;由![]() ,得
,得![]() ,即
,即![]() 时
时![]() 的图象过原点,故④正确.∴正确命题的序号是④,故答案为④.
的图象过原点,故④正确.∴正确命题的序号是④,故答案为④.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查三角函数函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,对存在性问题可以用特值法进行排除,还要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


科目:高中数学 来源: 题型:
【题目】已知点A(1,﹣1),B(4,0),C(2,2),平面区域D是所有满足 ![]() =
= ![]() +μ
+μ ![]() (1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
(1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
A.5
B.4 ![]()
C.9
D.5+4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}为等差数列,且a5=14,a7=20,数列{bn}的前n项和为Sn , b1= ![]() 且3Sn=Sn﹣1+2(n≥2,n∈N).
且3Sn=Sn﹣1+2(n≥2,n∈N).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn , n=1,2,3,…,Tn为数列{cn}的前n项和,Tn<m对n∈N*恒成立,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:
(1)求该班全体男生的人数;
(2)求分数在![]() 之间的男生人数,并计算频率公布直方图中
之间的男生人数,并计算频率公布直方图中![]() 之间的矩形的高;
之间的矩形的高;
(3)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
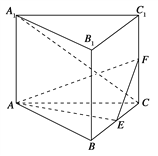
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为![]() ,
,![]() ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为![]() ,AC=0.1km。
,AC=0.1km。

(Ⅰ)试探究图中B,D间的距离与另外哪两点间距离会相等?
(II)求B,D间的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com