
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
【答案】(1)![]() ;(2)0.
;(2)0.
【解析】
(1)先求得A,B两点坐标,利用计算![]() 的周长可得p,进而求得抛物线方程;
的周长可得p,进而求得抛物线方程;
(2)利用导数的几何意义求得切线![]() 与
与![]() 的方程,联立直线与抛物线方程,利用韦达定理及
的方程,联立直线与抛物线方程,利用韦达定理及![]() 与
与![]() 的交点P,可得
的交点P,可得![]() ,再利用焦半径公式求得
,再利用焦半径公式求得![]() ,可得结果.
,可得结果.
(1)由题意知焦点![]() 的坐标为
的坐标为![]() ,将
,将![]() 代入抛物线
代入抛物线![]() 的方程可求得点
的方程可求得点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
有![]() ,
,![]() ,可得
,可得![]() 的周长为
的周长为![]() ,有
,有![]() ,得
,得![]() .
.
故抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)知抛物线![]() 的方程可化为
的方程可化为![]() ,求导可得
,求导可得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() .
.
设直线![]() 的方程为
的方程为![]() (直线
(直线![]() 的斜率显然存在).
的斜率显然存在).
联立方程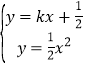 消去
消去![]() 整理为:
整理为:![]() ,可得
,可得![]() .
.
有![]() ,
,![]() .
.
可得直线![]() 的方程为
的方程为![]() ,整理为
,整理为![]() .
.
同理直线![]() 的方程为
的方程为![]() .
.
联立方程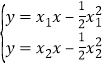 ,解得
,解得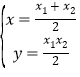 ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
由抛物线的几何性质知![]() ,
,![]() ,
,
![]() .
.
有![]()
![]() .
.
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某同学假期社会实践活动选定的课题是“节约用水研究”.为此他购买了电子节水阀,并记录了家庭未使用电子节水阀20天的日用水量数据(单位:![]() )和使用了电子节水阀20天的日用水量数据,并利用所学的《统计学》知识得到了未使用电子节水阀20天的日平均用水量为0.48
)和使用了电子节水阀20天的日用水量数据,并利用所学的《统计学》知识得到了未使用电子节水阀20天的日平均用水量为0.48![]() ,使用了电子节水阀20天的日用水量数据的频率分布直方图如下图:
,使用了电子节水阀20天的日用水量数据的频率分布直方图如下图:
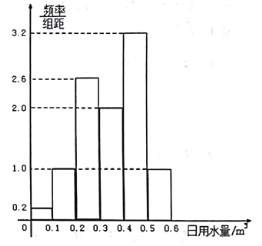
(1)试估计该家庭使用电子节水阀后,日用水量小于0.35![]() 的概率;
的概率;
(2)估计该家庭使用电子节水阀后,一年能节省多少![]() 水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在工业生产中,对一正三角形薄钢板(厚度不计)进行裁剪可以得到一种梯形钢板零件,现有一边长为3(单位:米)的正三角形钢板(如图),沿平行于边![]() 的直线
的直线![]() 将
将![]() 剪去,得到所需的梯形钢材
剪去,得到所需的梯形钢材![]() ,记这个梯形钢板的周长为
,记这个梯形钢板的周长为![]() (单位:米),面积为
(单位:米),面积为![]() (单位:平方米).
(单位:平方米).
(1)求梯形![]() 的面积
的面积![]() 关于它的周长
关于它的周长![]() 的函数关系式;
的函数关系式;
(2)若在生产中,梯形![]() 的面积与周长之比(即
的面积与周长之比(即![]() )达到最大值时,零件才能符合使用要求,试确定这个梯形的周长
)达到最大值时,零件才能符合使用要求,试确定这个梯形的周长![]() 为多时,该零件才可以在生产中使用?
为多时,该零件才可以在生产中使用?
查看答案和解析>>
科目:高中数学 来源: 题型:
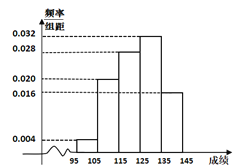
【题目】半期考试后,班长小王统计了50名同学的数学成绩,绘制频率分布直方图如图所示.
![]() 根据频率分布直方图,估计这50名同学的数学平均成绩;
根据频率分布直方图,估计这50名同学的数学平均成绩;
![]() 用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在
用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘轮船在航行中燃料费和它的速度的立方成正比.已知速度为每小时10千米时,燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问轮船的速度是多少时,航行1千米所需的费用总和最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有男性职工64名,一次体检后,将他们的体重(单位:kg)分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制出频率分布直方图如图,图中从左到右的前3个小组的频率之比为
,绘制出频率分布直方图如图,图中从左到右的前3个小组的频率之比为![]() .
.

(1)求这64名男职工中,体重小于60kg的人数;
(2)从体重在![]() kg范围的男职工中用分层抽样的方法选取6名,再从这6名男职工中随机选取2名,记“至少有一名男职工体重大于65kg”为事件
kg范围的男职工中用分层抽样的方法选取6名,再从这6名男职工中随机选取2名,记“至少有一名男职工体重大于65kg”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 在圆柱
在圆柱![]() 的底面
的底面![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的直径,且
的直径,且![]() .若圆柱
.若圆柱![]() 的体积
的体积![]() ,
,![]() ,
,![]() ,回答下列问题:
,回答下列问题:
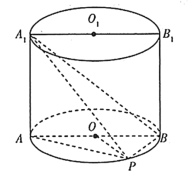
(1)求三棱锥![]() 的体积.
的体积.
(2)在线段AP上是否存在一点M,使异面直线OM与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,请指出点M的位置,并证明;若不存在,请说明理由.
?若存在,请指出点M的位置,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=![]() AC,AE=
AC,AE=![]() AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
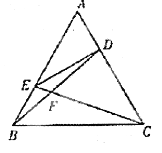
(Ⅰ)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com