【题目】已知{an}是等差数列，Sn是其前n项和，
（1）a2=﹣1，S15=75，求an与Sn；
（2）a1+a2+a3+a4=124，an+an﹣1+an﹣2+an﹣3=156，Sn=210，求项数n．
【答案】
（1）解：∵{an}是等差数列，Sn是其前n项和，a2=﹣1，S15=75，
∴ 
，
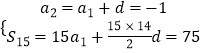解得a1=﹣2，d=1，
∴an=﹣2+（n﹣1）×1=n﹣3．
Sn= 
= 
．
（2）解：∵{an}是等差数列，Sn是其前n项和，
a1+a2+a3+a4=124，an+an﹣1+an﹣2+an﹣3=156，Sn=210，
∴4（a1+an）=（a1+a2+a3+a4+an+an﹣1+an﹣2+an﹣3）=124+156=280，
∴a1+an=70，
∴ 
= 
，
解得n=6．
【解析】（1）利用等差数列前n项和公式和通项公式列出方程组，求出首项和公差，由此能求出an与Sn ． （2）利用等差数列的通项公式得4（a1+an）=（a1+a2+a3+a4+an+an﹣1+an﹣2+an﹣3），从而求出a1+an=70，由此能求出项数n．
【考点精析】认真审题，首先需要了解等差数列的前n项和公式(前n项和公式：
)．
科目：高中数学 来源： 题型：
【题目】原命题：“
， 
为两个实数，若
，则
， 
中至少有一个不小于1”，下列说法错误的是（ ）
A. 逆命题为：若
， 
中至少有一个不小于1，则
，为假命题
B. 否命题为：若
，则
， 
都小于1，为假命题
C. 逆否命题为：若
， 
都小于1，则
，为真命题
D. “
”是“
， 
中至少有一个不小于1”的必要不充分条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】解答
（1）求函数f（x）= 
（x＜﹣1）的最大值，并求相应的x的值．
（2）已知正数a，b满足2a2+3b2=9，求a 
的最大值并求此时a和b的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列{an}的前n项和为Sn ， 设an是Sn与2的等差中项，数列{bn}中，b1=1，点P（bn ， bn+1）在直线y=x+2上．
（1）求an ， bn；
（2）若数列{bn}的前n项和为Bn ， 比较 
+ 
+…+ 
与1的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线 
的左、右焦点分别为F1、F2 ， P为C的右支上一点，且|PF2|=|F1F2|，则 
等于（ ）
A.24
B.48
C.50
D.56
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
