
【题目】天气预报说,未来三天每天下雨的概率都是0.6,用1、2、3、4表示不下雨,用5、6、7、8、9、0表示下雨,利用计算机生成下列20组随机数,则未来三天恰有两天下雨的概率大约是 .
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289.
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
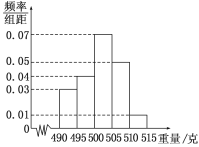
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三内角A,B,C所对的边分别是a,b,c,△ABC的面积S= ![]() 且sinA=
且sinA= ![]() .
.
(1)求sinB;
(2)若边c=5,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记集合A={(x,y)|x2+y2≤16}和集合B={(x,y)|x+y﹣4≤0,x≥0,y≥0}表示的平面区域分别为Ω1 , Ω2 , 若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(2)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同, 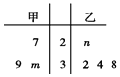
(1)求m,n的取值.
(2)比较甲、乙两组数据的稳定性,并说明理由.
注:方差公式s2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1 , 连接AP交棱CC1于点D.以A1为坐标原点建立空间直角坐标系,如图所示.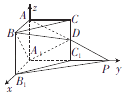
(1)写出A1、B、B1、C、D、P的坐标;
(2)求异面直线A1B与PB1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a1=﹣2,公差d=3;数列{bn}中,Sn为其前n项和,满足:2nSn+1=2n(n∈N+)
(Ⅰ)记An= ![]() ,求数列An的前n项和S;
,求数列An的前n项和S;
(Ⅱ)求证:数列{bn}是等比数列;
(Ⅲ)设数列{cn}满足cn=anbn , Tn为数列{cn}的前n项积,若数列{xn}满足x1=c2﹣c1 , 且xn= ![]() ,求数列{xn}的最大值.
,求数列{xn}的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com