
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续![]() 天,每天新增疑似病例不超过
天,每天新增疑似病例不超过![]() 人”.过去
人”.过去![]() 日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:总体平均数![]() ,且中位数为
,且中位数为![]() ;
;
乙地:总体平均数为![]() ,且标准差
,且标准差![]() ;
;
丙地:总体平均数![]() ,且极差
,且极差![]() ;
;
丁地:众数为![]() ,且极差
,且极差![]() .
.
A.甲地B.乙地C.丙地D.丁地
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
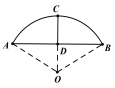
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为![]() ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )
A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照经验公式计算所得弧田面积(![]() )平方米
)平方米
C. 按照弓形的面积计算实际面积为(![]() )平方米
)平方米
D. 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: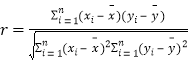 ,回归直线方程是
,回归直线方程是![]() ,
,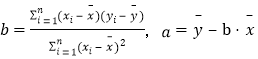 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ),
),![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的单调区间和极值;
的单调区间和极值;
(2)若对任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若函数![]() 在
在![]() 上是增函数,求正数
上是增函数,求正数![]() 的取值范围;
的取值范围;
(2)当![]() 时,设函数
时,设函数![]() 的图象与x轴的交点为
的图象与x轴的交点为![]() ,
,![]() ,曲线
,曲线![]() 在
在![]() ,
,![]() 两点处的切线斜率分别为
两点处的切线斜率分别为![]() ,
,![]() ,求证:
,求证:![]() +
+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知4名学生和2名教师站在一排照相,求:
(1)中间二个位置排教师,有多少种排法?
(2)首尾不排教师,有多少种排法?
(3)两名教师不站在两端,且必须相邻,有多少种排法?
(4)两名教师不能相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②B. ①③④C. ②④D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com