
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |
分析 令g(x)=f(x)cosx,则g′(x)=f′(x)cosx-f(x)sinx>0,当0<x<π时,g(x)在(0,π)递增,即可判断出结论.
解答 解:令g(x)=f(x)cosx,则g′(x)=f′(x)cosx-f(x)sinx>0,
当0<x<π时,g(x)在(0,π)递增,
∵$0<\frac{π}{3}<\frac{π}{2}$<$\frac{5π}{6}$<π,
∴$cos\frac{π}{3}$$f(\frac{π}{3})$<$cos\frac{π}{2}f(\frac{π}{2})$<$cos\frac{5π}{6}f(\frac{5π}{6})$,
化为:$\frac{1}{2}$$f(\frac{π}{3})$<0<$-\frac{\sqrt{3}}{2}$$f(\frac{5π}{6})$,
即a<b<c.
故选:A.
点评 本题考查了构造函数方法、利用导数研究函数的单调性、三角函数求值考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
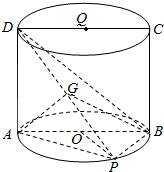 如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.
如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 以上情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | [-1,2] | C. | [-3,2] | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$+y2=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,α∩β=n,则m∥n | B. | 若α⊥β,m⊥α,n⊥β,则m⊥n | ||
| C. | 若α⊥β,α⊥γ,β∩γ=m,则m⊥α | D. | 若α∥β,m∥α,则m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 8 | C. | $\frac{13}{2}$ | D. | $\frac{11}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com