[题目]如图.正方形中. . 与交于点.现将沿折起得到三棱锥. . 分别是. 的中点.(1)求证: ,(2)若三棱锥的最大体积为.当三棱锥的体积为.且为锐角时.求三棱锥的体积. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，正方形中，，与交于点，现将沿折起得到三棱锥，，分别是，的中点.

(1)求证：；

(2)若三棱锥的最大体积为，当三棱锥的体积为，且为锐角时，求三棱锥的体积.

【答案】(1)证明见解析；(2) .

【解析】试题分析：（1）根据折叠前几何关系得，，再根据线面垂直判定定理得平面，即得；（2）先确定三棱锥的取最大体积的条件：三棱锥的高为，再根据三棱锥体积公式得三棱锥的体积为时条件：平面，最后根据等体积法求三棱锥的体积.

试题解析：(1)依题意易知，，，∴平面，

又∵平面，∴.

(2)当体积最大时三棱锥的高为，当体积为时，高为，

中，，作于，∴，∴，

∴为等边三角形，∴与重合，即平面，

易知.

∵平面，∴，∴，

∴.

练习册系列答案

初中学业考试复习学与练指导丛书系列答案

考点解析与知能训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】近年来，空气质量成为人们越来越关注的话题，空气质量指数（，Air Quality Inder简称）是定量描述空气质量状况的指数，空气质量按照大小分为六级，为优；为良；为轻度污染；为中度污染；为重度污染；大于300为严重污染．环保部门记录了2017年某月哈尔滨市10天的的茎叶图如下：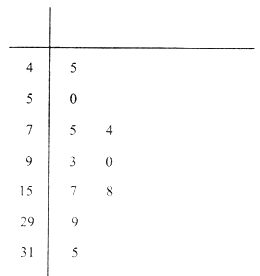

（1）利用该样本估计该地本月空气质量优良（）的天数；（按这个月总共30天计算）
（2）现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究，求抽取的2天中至少有一天空气质量是优的概率；
（3）将频率视为概率，从本月中随机抽取3天，记空气质量优良的天数为，求的概率分布列和数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知n为正整数，在二项式（ +2x）n的展开式中，若前三项的二项式系数的和等于79．
（1）求n的值；
（2）判断展开式中第几项的系数最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本题满分12分）甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：

甲 82 81 79 78 95 88 93 84

乙 92 95 80 75 83 80 90 85

（1）用茎叶图表示这两组数据；

（2）现要从中选派一人参加数学竞赛，从统计学的角度（在平均数、方差或标准差中选两个）分析，你认为选派哪位学生参加合适？请说明理由

参考公式：

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】【2018海南高三阶段性测试（二模）】如图，在直三棱柱中，，，点为的中点，点为上一动点．

（I）是否存在一点，使得线段平面？若存在，指出点的位置，若不存在，请说明理由．

（II）若点为的中点且，求三棱锥的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列四个结论： ①若x＞0，则x＞sinx恒成立；
②“若am2＜bm2 ，则a＜b”的逆命题为真命题
③m∈R，使f（x）=（m﹣1）x 是幂函数，且在（﹣∞，0）上单调递减
④对于命题p：x∈R使得x2+x+1＜0，则￢p：x∈R，均有x2+x+1＞0
其中正确结论的个数是（）
A.1个
B.2个
C.3个
D.4个