
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|1﹣![]() |
|
(1)求满足f(x)=2的x值;
(2)是否存在实数a,b,且0<a<b<1,使得函数y=f(x)在区间[a,b]上的值域为[a,2b],若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直线PQ与⊙O切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于Q点.
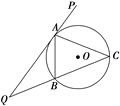
(1)求证:QC·AC=QC2-QA2;
(2)若AQ=6,AC=5,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=![]() , g(x)是二次函数,若f(g(x))的值域是[0,+∞),则函数g(x)的值域是( )
, g(x)是二次函数,若f(g(x))的值域是[0,+∞),则函数g(x)的值域是( )
A.(﹣∞,﹣1]∪[1,+∞)
B.(﹣∞,﹣1]∪[0,+∞)
C.[0,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线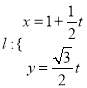 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=af(x)﹣1(a>0且a≠1).
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[﹣1,2]上的最大值;
(Ⅲ)当a=![]() 时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,它们在
,它们在![]() 轴右侧有两个交点
轴右侧有两个交点![]() 、
、![]() ,满足
,满足![]() .将直线
.将直线![]() 左侧的椭圆部分(含
左侧的椭圆部分(含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() ,直线
,直线![]() 右侧的双曲线部分(不含
右侧的双曲线部分(不含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() .以
.以![]() 为端点作一条射线,分别交
为端点作一条射线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (点
(点![]() 在第一象限),设此时
在第一象限),设此时![]() .
.
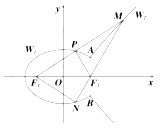
(1)求![]() 的方程;
的方程;
(2)证明: ![]() ,并探索直线
,并探索直线![]() 与
与![]() 斜率之间的关系;
斜率之间的关系;
(3)设直线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com