
【题目】在直角坐标![]() 中,圆
中,圆![]() ,圆
,圆![]() 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆![]() 的公共弦的参数方程。
的公共弦的参数方程。
科目:高中数学 来源: 题型:
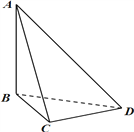
【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,则三棱锥
,则三棱锥![]() 的外接球的球面面积为__________.
的外接球的球面面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018吉林长春高三下学期二模】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如下图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
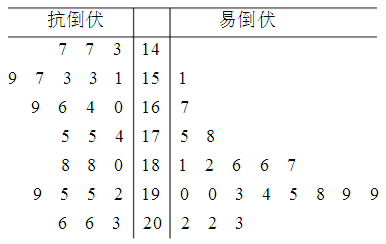
(I)完成列![]() 联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(II)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示。
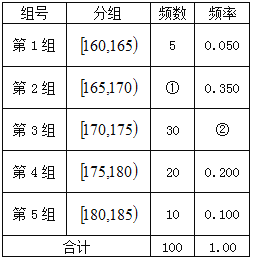
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A教官进行面试,求:第4组至少有一名学生被考官A面试的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com