函数f(x)的定义域为D={x|x>0},满足:对于任意m,n∈D,都有f(mn)=f(m)+f(n),且f(2)=1.
(1)求f(4)的值;(2)如果f(2x-6)≤3,且f(x)在(0,+∞)上是单调增函数,求x的取值范围.
【答案】
分析:(1)由已知中对于任意m,n∈D,都有f(mn)=f(m)+f(n),且f(2)=1,令m=n=2,易求出f(4)的值;
(2)结合(1)中f(2)=1,f(4)=2及f(mn)=f(m)+f(n),可得f(8)=3,结合f(x)在(0,+∞)上是单调增函数,可将不等式f(2x-6)≤3转化为不等式组
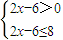
解不等式组,即可得到答案.
解答:解:(1)∵对于任意m,n∈D,都有f(mn)=f(m)+f(n),且f(2)=1
令m=n=2
则f(4)=f(2)+f(2)=2,
(2)∵f(2)=1,f(4)=2
∴f(8)=f(2)+f(4)=3,
又∵f(x)在(0,+∞)上是单调增函数,
∴f(2x-6)≤3成立时,x满足

解得:3<x≤7
即满足条件的x的取值范围为3<x≤7
点评:本题考查的知识点是抽象函数及其应用,其中根据已知中函数的解析式,利用凑配法,求出f(4)=2,f(8)=3等,是解答本题的关键.

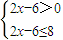 解不等式组,即可得到答案.
解不等式组,即可得到答案.


 名校课堂系列答案
名校课堂系列答案