
【题目】已知椭圆![]() 的焦点到短轴的端点的距离为
的焦点到短轴的端点的距离为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由题意可得![]() ,由离心率公式可得
,由离心率公式可得![]() ,再由
,再由![]() 的关系可得
的关系可得![]() ,即可得到所求的椭圆方程;
,即可得到所求的椭圆方程;
(2)先求出直线![]() 的斜率不存在时直线
的斜率不存在时直线![]() 的方程,直线
的方程,直线![]() 过点
过点![]() ;当直线
;当直线![]() 的斜率存在,设过点
的斜率存在,设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,联立椭圆方程,运用韦达定理,以及直线的斜率公式,结合三点共线的条件,即可得到定点且定点为
,联立椭圆方程,运用韦达定理,以及直线的斜率公式,结合三点共线的条件,即可得到定点且定点为![]() .
.
(1)由椭圆![]() 的焦点到短轴的端点的距离为
的焦点到短轴的端点的距离为![]() ,则
,则![]() ,
,
又离心率为![]() ,即
,即![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:当直线![]() 的斜率不存在,即方程
的斜率不存在,即方程![]() ,
,
代入椭圆方程可得![]() ,即有
,即有![]() ,
,
直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 过点
过点![]() .
.
当直线![]() 的斜率存在,设过点
的斜率存在,设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,
由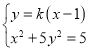 ,消去
,消去![]() 整理得
整理得![]() .
.
由![]() 恒成立,
恒成立,
设![]() ,
,
则![]() ①,
①,![]() ②,
②,
![]() ,
,
由![]() ,
,
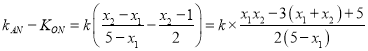
由①②可得![]() ,
,
则![]() ,即
,即![]()
综上可得直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】如图①,已知矩形ABCD满足AB=5,![]() ,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱
,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱![]() .
.

⑴若图②中△ABG是直角三角形,这里G是线段EF上的点,试求线段EG的长度x的取值范围;
⑵若⑴中EG的长度为取值范围内的最大整数,且线段AB的长度取得最小值,求二面角![]() 的值;
的值;
⑶在⑴与⑵的条件都满足的情况下,求三棱锥A-BFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数![]() 满足
满足![]() ,现给出下列命题:①函数
,现给出下列命题:①函数![]() 是以2为周期的周期函数;②函数
是以2为周期的周期函数;②函数![]() 是以4为周期的周期函数;③函数
是以4为周期的周期函数;③函数![]() 为奇函数;④函数
为奇函数;④函数![]() 为偶函数,则其中真命题的个数是( )
为偶函数,则其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了反映国民经济各行业对仓储物流业务的需求变化情况,以及重要商品库存变化的动向,中国物流与采购联合会和中储发展股份有限公司通过联合调查,制定了中国仓储指数.如图所示的折线图是2016年1月至2017年12月的中国仓储指数走势情况.

根据该折线图,下列结论正确的是
A. 2016年各月的仓储指数最大值是在3月份
B. 2017年1月至12月的仓储指数的中位数为54%
C. 2017年1月至4月的仓储指数比2016年同期波动性更大
D. 2017年11月的仓储指数较上月有所回落,显示出仓储业务活动仍然较为活跃,经济运行稳中向好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
①存在某个位置,使得![]() ;
;
②翻折过程中,![]() 的长是定值;
的长是定值;
③若![]() ,则
,则![]() ;
;
④若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费对产品进行促销,在一年内,预计年销量![]() (万件)与广告费
(万件)与广告费![]() (万元)之间的函数关系为
(万元)之间的函数关系为![]() ,已知生产此产品的年固定投入为
,已知生产此产品的年固定投入为![]() 万元,每生产
万元,每生产![]() 万件此产品仍需要投入
万件此产品仍需要投入![]() 万元,若年销售额为“年生产成本的
万元,若年销售额为“年生产成本的![]() ”与“年广告费的
”与“年广告费的![]() ”之和,而当年产销量相等:
”之和,而当年产销量相等:
(1)试将年利润![]() (万元)表示为年广告费
(万元)表示为年广告费![]() (万元)的函数;
(万元)的函数;
(2)求当年广告费投入多少万元时,企业利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com