
设
y=f(x)是R上的奇函数.f(x
+2)=-f(x).当-1≤x≤1时,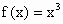 .
.
(1)
试证:直线x=1是函数y=f(x)图象的对称轴;(2)
试求xÎ [1,5)时,f(x)解析式;(3)
若A={x||f(x)|>a,xÎ R,且 ,求实数a的取值范围.
,求实数a的取值范围.
|
(1) ∵f(1+x)=f[2+(x-1)]=-f(x-1)=f(1-x),∴ y=f(x)的图象关于直线x=1对称.(2) 当xÎ [1,3]时,2-xÎ [-1,1],则 当 xÎ [3,5]时,x-2Î [1,3],则 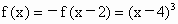 . .
∴ 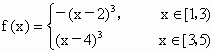
(3)f(x +4)=-f(x+2)=f(x),∴ f(x)是以4为周期的函数.∴ {y|y=f(x),xÎ R}={y|y=f(x),1≤x≤5},∵ f(x)在[1,3]上是减函数,∴-1≤f(x)≤1;又 f(x)在[3,5]上是增函数,∴- 1≤f(x)≤1,∴f(x)的值域为[-1,1],即 |f(x)|≤1,故a<1. |


科目:高中数学 来源:数学教研室 题型:044
设y=f(x)是R上的奇函数.
f(x+2)=-f(x).当-1≤x≤1时,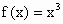 .
.
(1)试证:直线x=1是函数y=f(x)图象的对称轴;
(2)试求xÎ [1,5)时,f(x)解析式;
(3)若A={x||f(x)|>a,xÎ
R,且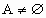 ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省长葛市高二下学期3月月考数学理卷A 题型:选择题
.设函数f(x)是R上以5为周期的可导偶函数,则曲线y=f(x)在x=5处的切线的斜率为( )
A.- B.0 C.
B.0 C. D.5
D.5
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(江西) 题型:选择题
设函数f(x)是R上以5为周期的可导偶函数,则曲线y=f(x)在x=5处的切线的斜率为
A.-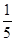 B.0 C.
B.0 C.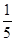 D.5
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com