
【题目】解答题。
(1)作出不等式x+y﹣3≤0在坐标平面内表示的区域(用阴影部分表示);
(2)求不等式x2﹣3x+2<0的解集.
【答案】
(1)解:不等式x+y﹣3≤0在坐标平面内表示的区域,如图所示
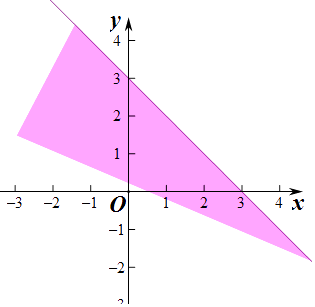
(2)解:不等式x2﹣3x+2<0,可化为(x﹣1)(x﹣2)<0,
∴1<x<2,
∴不等式x2﹣3x+2<0的解集为{x|1<x<2}
【解析】(1)根据不等式,可得不等式x+y﹣3≤0在坐标平面内表示的区域;(2)不等式x2﹣3x+2<0,可化为(x﹣1)(x﹣2)<0,即可求不等式x2﹣3x+2<0的解集.
【考点精析】利用解一元二次不等式和二元一次不等式(组)所表示的平面区域对题目进行判断即可得到答案,需要熟知求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;不等式组表示的平面区域是各个不等式所表示的平面区域的公共部.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;不等式组表示的平面区域是各个不等式所表示的平面区域的公共部.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0,
=1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0, ![]() ),则e的取值范围是 .
),则e的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1的左、右焦点分别为F1 , F2 , 直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1于点P,线段PF2的垂直平分线与l1的交点的轨迹为曲线C2 , 若点Q是C2上任意的一点,定点A(4,3),B(1,0),则|QA|+|QB|的最小值为( )
=1的左、右焦点分别为F1 , F2 , 直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1于点P,线段PF2的垂直平分线与l1的交点的轨迹为曲线C2 , 若点Q是C2上任意的一点,定点A(4,3),B(1,0),则|QA|+|QB|的最小值为( )
A.6
B.3 ![]()
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体OABC﹣O′A′B′C′中,E,F分别是棱AB,BC上的动点. 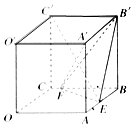
(1)当AE=BF时,求证A′F⊥C′E;
(2)若E,F分别为AB,BC的中点,求直线O′B与平面B′EF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率;
(Ⅱ)已知每检测一件产品需要费用100元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司10位员工的月工资(单位:元)为x1 , x2 , …,x10 , 其均值和方差分别为 ![]() 和s2 , 若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
和s2 , 若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
A.![]() ,s2+1002
,s2+1002
B.![]() +100,s2+1002
+100,s2+1002
C.![]() ,s2
,s2
D.![]() +100,s2
+100,s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三项式(x2+x+1)n展开,当n=1,2,3,…时,得到如下所示的展开式,如图所示的广义杨辉三角形: (x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
观察多项式系数之间的关系,可以仿照杨辉三角形构造如图所示的广义杨辉三角形,其构造方法:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(a+x)(x2+x+1)4的展开式中,x6项的系数为46,则实数a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少有一次得满分的学生有15名,若后两次均为满分的学生至少有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com