
����Ŀ����ͼ���ı���ABCD�У�AB��AD��AD��BC��AD��6��BC��2AB��4��E��F�ֱ���BC��AD�ϣ�EF��AB.�ֽ��ı���ABCD��EF����ʹƽ��ABEF��ƽ��EFDC.
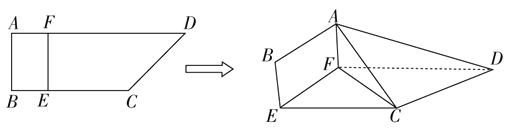
������BE��1���Ƿ����۵�����߶�AD�ϴ���һ��P����![]() ��ʹCP��ƽ��ABEF�������ڣ��������ֵ���������ڣ�˵�����ɣ�
��ʹCP��ƽ��ABEF�������ڣ��������ֵ���������ڣ�˵�����ɣ�
������������A��CDF����������ֵ���������ʱ�����E��AC��F������ֵ��
���𰸡���1����������2��![]()
���������������:��1������P��MP��FD��AF�ڵ�M����MP=CE,���ı���MPCEΪƽ���ı��Σ�����CP��ME��Ҳ�͵�CP��ƽ��ABEF,��������Ʊȿɵ�����ֵ����2�������洹ֱ���ʶ�����AF��ƽ��EFDC,����AFΪ��,�������������ʽ�Լ���������ʽ�ɵ�������ֵ;��E��EO��CF,����������߶����ɵ�AO��CF,����AOEΪ�����E��AC��F��ƽ���,���ͨ���������ε�����ֵ
�����������ƽ��ABEF��ƽ��EFDC��ƽ��ABEF��ƽ��EFDC��EF��FD��EF��
��FD��ƽ��ABEF����AFƽ��ABEF��
��FD��AF��
�����������AF��EF����FD��EF��F��
��AF��ƽ��EFDC.
��FΪԭ�㣬FE��FD��FA�ֱ�Ϊx��y��z�Ὠ���ռ�ֱ������ϵ��
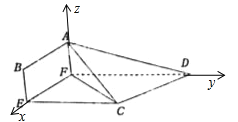 ��I���ⷨһ����BE��1��������������£�
��I���ⷨһ����BE��1��������������£�
F(0,0,0)��A(0,0,1)��D(0,5,0)��C(2,3,0)��
��ƽ��ABEF�ķ�������Ϊ![]() ��(0,5,0)��
��(0,5,0)��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ����(
����(![]() ��
��![]() )��
)��
��![]() ��
��![]()
![]() ��
��![]()
![]() ��
��![]() (0,0,1)��
(0,0,1)��![]() (0,5,0)��
(0,5,0)��![]() ��
��
��P![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��CP��ƽ��ABEF�������![]() ��
��![]() ����
����![]() ��
��![]() ��0��
��0��
��![]() ��
��![]() ��
��![]() ��(0,5,0)��
��(0,5,0)��![]() ��5��0��
��5��0��
������![]() ��
��
��AD�ϴ���һ��P����![]() ��
��![]()
![]() ��ʹCP��ƽ��ABEF.
��ʹCP��ƽ��ABEF.
�ⷨ����AD�ϴ���һ��P��ʹCP��ƽ��ABEF����ʱ����![]() .�������£�
.�������£�
������![]() ʱ��
ʱ��![]() ��
��![]()
![]() ����֪
����֪![]() ��
��![]() ��
��
����P��MP��FD��AF�ڵ�M������EM��PC������![]() ��
��![]() ��
��![]() ��
��
��BE��1���ɵ�FD��5����MP��3��
��EC��3��MP��FD��EC������MP��EC�����ı���MPCEΪƽ���ı��Σ�
��CP��ME����CPƽ��ABEF��MEƽ��ABEF��
����CP��ƽ��ABEF.
��II����BE
��V����A��CDF��![]() ��
��![]() ��2��(6��x)��x��
��2��(6��x)��x��![]() (��x2��6x)��
(��x2��6x)��
�൱x��3ʱ��V����A��CDF�����ֵ�������ֵΪ3��
��A(0,0,3)��D(0,3,0)��C(2,1,0)��E(2,0,0)��
��![]() ��(2,0����3)��
��(2,0����3)��![]() ��(2,1����3)��
��(2,1����3)��![]() ��(0,0,3)��
��(0,0,3)��![]() ��(2,1,0)��
��(2,1,0)��
��ƽ��ACE�ķ�����m��(x1��y1��z1)��
��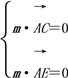 ����
����![]() ��
��
��x1��3����y1��0��z1��2����m��(3,0,2)��
��ƽ��ACF�ķ�����n��(x2��y2��z2)��
��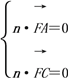 ����
����![]() ��
��
��x2��1����y2����2��z2��0����n��(1����2,0)��
��cos��m��n����![]() ��
��![]() ��
��![]() ��
��
�ʶ����E��AC��F������ֵΪ![]() .
.


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1������f��x���ĵ��������䣻
��2���� ![]() ����cos2����ֵ��
����cos2����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��A1B1C1D1�У�E��F��G��H�ֱ�ΪAA1 �� AB��BB1 �� B1C1���е㣬������ֱ��EF��GH���ɵĽǵ��ڣ� �� 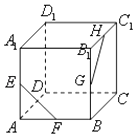
A.45��
B.60��
C.90��
D.120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵ�ż����f��x������f��x+2��=f��x��������[��3����2]���Ǽ�������������������������ε������ڽǣ��� ��
A.f��sin������f��sin�£�
B.f��sin������f��cos�£�
C.f��cos������f��cos�£�
D.f��sin������f��cos�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x3+ax2+��a+6��x+1�м���ֵ�ͼ�Сֵ����a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��3x+alnx��a��0���� ������a=1������f��x���ĵ�������ͼ�ֵ��
�����躯��f��x��ͼ��������һ�������l��б��Ϊk����k����СֵΪ1ʱ�����ʱ����l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У�
�� ![]() �������
�������![]() ������ֵ��
������ֵ��![]() ����������������ı�������� ��
����������������ı�������� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ͷ��81��Ԫ��һ�乤���ң���һ��װ��Ϊ1��Ԫ���Ժ�ÿ������2��Ԫ���ѹ����ҳ��⣬ÿ���������30��Ԫ��
(1)���۳�Ͷ�ʺ���װ�ѣ���ӵڼ��꿪ʼ��ȡ������
(2)������������Ϊ��Ͷ��������Ŀ���Ըù����������ִ�������������ƽ���������ʱ����46��Ԫ���۸ù����ң����������ܺ����ʱ����10��Ԫ���۸ù����ң��ʸ����˻�ѡ�����ַ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=ax3+bx2+cx�ļ�СֵΪ��8���䵼����y=f�䣨x����ͼ���� ![]() ����ͼ��ʾ��
����ͼ��ʾ�� 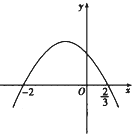
��1����f��x���Ľ���ʽ��
��2������x��[��3��3]����f��x����m2��14m���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com