
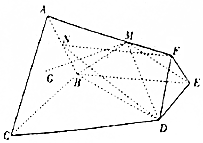
 如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.
如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.分析 (1)连AG延长交BC于P,推出$\frac{AG}{AP}=\frac{2}{3}$,证明GM∥PF,然后证明NP∥AC,推出NP∥DF,进一步证明GM∥平面DFN;
(2)由已知求出底面三角形BDE的面积,结合三棱锥M-BDE的体积求出M到底面的距离,由平行线截线段成比例可得λ的值.
解答  (1)证明:连AG延长交BC于P,
(1)证明:连AG延长交BC于P,
∵点G为△ABC的重心,∴$\frac{AG}{AP}=\frac{2}{3}$,
又$\frac{AM}{AF}$=λ,∴$\frac{AG}{AP}=\frac{AM}{AF}=\frac{2}{3}$,
∴GM∥PF,
∵N为AB中点,P为BC中点,NP∥AC,又AC∥DF,
∴NP∥DF,得P、D、F、N四点共面,
∴GM∥平面DFN;
(2)解:∵BC=2,且P为BC中点,∴PC=1,
又CD=1,CD⊥CP,∴PD=$\sqrt{2}$,
在平行四边形BPDE中,可得${S}_{△BDE}=\frac{1}{2}×1×\sqrt{2}×sin135°=\frac{1}{2}$,
设M到平面BDE的距离为h,
∵VM-BDE=$\frac{\sqrt{3}}{9}$,
∴$\frac{1}{3}×\frac{1}{2}×h=\frac{\sqrt{3}}{9}$,得h=$\frac{2\sqrt{3}}{3}$.
又∵F到平面BDE的距离为$\frac{\sqrt{3}}{2}$,A到平面BDE的距离为$\sqrt{3}$,
∴$\frac{FM}{AF}=\frac{\frac{2\sqrt{3}}{3}-\frac{\sqrt{3}}{2}}{\sqrt{3}-\frac{2\sqrt{3}}{3}}=\frac{1}{2}$,
∴$\frac{AM}{AF}=λ=\frac{1}{2}$.
点评 本题考查直线与平面平行的判定,考查了空间想象能力和思维能力,训练了平行线截线段成比例的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | log29 | D. | log27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\sqrt{2}$ | B. | x=-2$\sqrt{2}$ | C. | x=-2 | D. | x=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [12,24] | B. | [12,25] | C. | [6,12] | D. | [6,$\frac{25}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3:\sqrt{10}$ | B. | $1:\sqrt{10}$ | C. | 1:2 | D. | 1:3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com