
 +1,其中a为实数:
+1,其中a为实数: ,求a的值.
,求a的值. +1,定义域为(0,+∞),x>0,知
+1,定义域为(0,+∞),x>0,知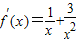 ,由此能够证明f(x)在定义域(0,+∞)内为增函数.
,由此能够证明f(x)在定义域(0,+∞)内为增函数.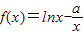 +1,知
+1,知 +
+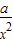 ,令f′(x)=0得x=-a,以-a在[1,e]内,左,右分为三类来讨论,函数在[1,e]上的单调性,进而求出最值,令其等于32,求出a的值,由范围来取舍,得出a的值.
,令f′(x)=0得x=-a,以-a在[1,e]内,左,右分为三类来讨论,函数在[1,e]上的单调性,进而求出最值,令其等于32,求出a的值,由范围来取舍,得出a的值.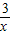 +1,定义域为(0,+∞),x>0,
+1,定义域为(0,+∞),x>0,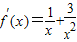
 >0,
>0,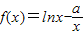 +1,
+1,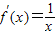 +
+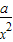 ,
,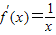 +
+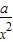 =0,得x=-a.
=0,得x=-a. ,a=-
,a=- <-1,不符题意,舍;
<-1,不符题意,舍; =
= ,a=-
,a=-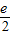 >-e,不符题意,舍;
>-e,不符题意,舍; ,a=-e
,a=-e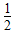 满足;
满足;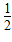 .
.

科目:高中数学 来源: 题型:
(1)判断函数y=logax的增减性;
(2)若命题p:|f(x)|<1-|f(2x)|为真命题,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市高三八校联考理科数学 题型:填空题
已知函数 ,
, ,其中a为常数,且函数y=f(x)和y=g(x)的图像在其与两坐标轴的交点处的切线相互平行.若关于x的不等式
,其中a为常数,且函数y=f(x)和y=g(x)的图像在其与两坐标轴的交点处的切线相互平行.若关于x的不等式 对任意不等于1的正实数都成立,则实数m的取值集合是____________。
对任意不等于1的正实数都成立,则实数m的取值集合是____________。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第一次月考试卷理科数学 题型:解答题
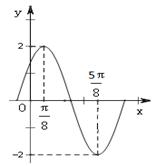
已知函数f(x)=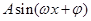 (其中A>0,
(其中A>0,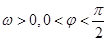 )的图象如图所示。
)的图象如图所示。
(1)求A,w及j的值;
(2)若tana=2,求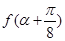 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com