
【题目】设数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将两个数列的偏差距离定义为
,则将两个数列的偏差距离定义为![]() ,其中
,其中![]() .
.
(1)求数列1,2,7,8和数列2,3,5,6的偏差距离;
(2)设![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,
的集合,![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() ,若
,若![]() ,
,![]() ,
,![]() 和
和![]() 的偏差距离小于2020,求
的偏差距离小于2020,求![]() 最大值;
最大值;
(3)记![]() 是所有7项数列
是所有7项数列![]() 或
或![]() 的集合,
的集合,![]() ,且
,且![]() 中任何两个元素的偏差距离大于或等于3,证明:
中任何两个元素的偏差距离大于或等于3,证明:![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
【答案】(1)6;(2)3461;(3)见解析.
【解析】
(1)由数列距离的定义即可求得数列1,2,7,8和数列2,3,5,6的偏差距离;
(2)由数列的递推公式,即可求得![]() 中数列的项周期性重复,且间隔4项重复一次,求得数列
中数列的项周期性重复,且间隔4项重复一次,求得数列![]() ,
,![]() 的规律,可知随着项数
的规律,可知随着项数![]() 越大,数列
越大,数列![]() ,
,![]() 的距离越大,由
的距离越大,由![]() ,再根据周期的定义得到
,再根据周期的定义得到![]() 的取大值;
的取大值;
(3)利用反证法,假设![]() 中的元素个数大于等于17个,设出
中的元素个数大于等于17个,设出![]() ,最后求得
,最后求得![]() 和
和![]() 中必有一个成立,与数列偏差距离大于或等于3相矛盾,故可证明
中必有一个成立,与数列偏差距离大于或等于3相矛盾,故可证明![]() 中的元素个数于于或等于16.
中的元素个数于于或等于16.
(1)由题意得,数列1,2,7,8和数列2,3,5,6的偏差距离为:![]() .
.
(2)设![]() ,其中
,其中![]() ,且
,且![]() ,
,
由![]() 得
得![]() ,所以
,所以![]() .
.
因此![]() 中数列的项周期性重复,且间隔4项重复一次,
中数列的项周期性重复,且间隔4项重复一次,
所以数列![]() 中,
中,![]() ,
,
所以数列![]() 中,
中,![]() ,
,
![]() 项数
项数![]() 越大,数列
越大,数列![]() ,
,![]() 的距离越大,
的距离越大,
由![]() ,
,
得![]() ,
,
故的最大值为![]() .
.
(3)假设![]() 中元素素个数大于等于17个,
中元素素个数大于等于17个,
因为数列![]() 中,
中,![]() 或
或![]() ,
,
所以仅由数列前三项组成的数组![]() 有且仅有8个,
有且仅有8个,
![]()
![]()
那么这17个元素(即数列)之中必有三个具有相同的![]() ,
,
设这个数列分别为![]()
![]() ,其中
,其中![]() ,
,
因为这三个数列中每两个的距离大于等于3,
所以,![]() 和
和![]() 中,
中,![]() 中至少有三个成立,
中至少有三个成立,
不妨设![]() ,
,
由题意,![]() 和
和![]() 中一个等于0,而另一个等于1,
中一个等于0,而另一个等于1,
又因为![]() 或
或![]() ,
,
所以![]() 和
和![]() 中必有一个成立,
中必有一个成立,
同理,得![]() 和
和![]() 中必有一个成立,
中必有一个成立,![]() 和
和![]() 中必有一个成立,
中必有一个成立,
所以“![]() 中至少有两个成立”或“
中至少有两个成立”或“![]() 中至少有两个成立”中必有一个成立,
中至少有两个成立”中必有一个成立,
所以![]() 和
和![]() 中必有一个成立,与题意矛盾,
中必有一个成立,与题意矛盾,
所以![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-4)ex+a(x+2)2(x>0,a∈R,e是自然对数的底数).
(1)若f(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)当a∈![]() 时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名,现从这5名被调查者中随机选取3名,求这3名被调查者中恰有1名对手机游戏无兴趣的概率.
附: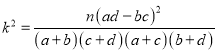
参考数据:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com