
【题目】已知四棱柱![]() 的底面是边长为
的底面是边长为![]() 的菱形,且
的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点为
中点为![]() ,求证四边形
,求证四边形![]() 为平行四边形,即可由线线平行推证线面平行;
为平行四边形,即可由线线平行推证线面平行;
(2)以![]() 为坐标原点,建立空间直角坐标系,通过求解两平面法向量之间夹角的余弦值,从而求得二面角夹角的余弦值.
为坐标原点,建立空间直角坐标系,通过求解两平面法向量之间夹角的余弦值,从而求得二面角夹角的余弦值.
(1)证明:∵![]() ,
,![]() ,∴
,∴![]() 是
是![]() 中点,
中点,
取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,如下图所示:
,如下图所示:
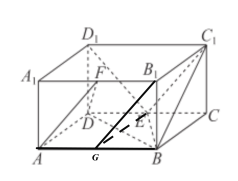
则在菱形![]() 中,
中,![]() ,
,![]() //
//![]()
∵![]() ,
,![]() //
//![]() ,∴
,∴![]() ,
,![]() //
//![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() //
//![]() ,
,
又![]() ,
,![]() //
//![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() //
//![]() ,∴
,∴![]() //
//![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() //平面
//平面![]() .即证.
.即证.
(2)以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 建立如图所示的空间的直角坐标系.
建立如图所示的空间的直角坐标系.
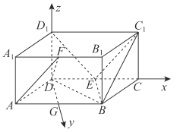
因为已知该四棱柱为直四棱柱,![]() ,
,![]() ,
,
所以![]() 为等边三角形.
为等边三角形.
因为![]() ,所以点
,所以点![]() 是
是![]() 的中点.
的中点.
故点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.
由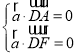 得
得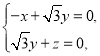
取![]() ,得
,得![]() ,
,![]() ,
,
故![]()
![]() .
.
∵![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
∴![]() ,∴
,∴![]() 是平面
是平面![]() 的法向量,
的法向量,
设平面![]() 和平面
和平面![]() 所成锐角为
所成锐角为![]() ,
,
则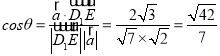 .
.
即平面![]() 和平面
和平面![]() 所成锐角的余弦值为
所成锐角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() =0(a>0),曲线
=0(a>0),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)已知极坐标方程为![]() =
=![]() 的直线与曲线
的直线与曲线![]() ,
,![]() 分别相交于P,Q两点(均异于原点O),若|PQ|=
分别相交于P,Q两点(均异于原点O),若|PQ|=![]() ﹣1,求实数a的值;
﹣1,求实数a的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数中:①
为“理想函数”.给出下列四个函数中:① ![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④ 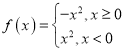 ,能被称为“理想函数”的有_____(请将所有正确命题的序号都填上).
,能被称为“理想函数”的有_____(请将所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(1)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)在上述样本中,学校从成绩为![]() 的学生中随机抽取
的学生中随机抽取![]() 人进行学习交流,求这
人进行学习交流,求这![]() 人来自同一个班级的概率.
人来自同一个班级的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com