
【题目】
如图所示的空间几何体,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为![]() .且点E在平面ABC上的射影落在
.且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.

(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明线面平行,需要证明直线平行面内的一条直线即可.
(2)利用三垂线定理作出二面角的平面角即可求解.
(3)求多面体ABCDE的体积,转化两个三棱锥的体积之和,分别求解
(1)由题意知,△ABC,△ACD都是边长为2的等边三角形,
取AC中点O,连接BO,DO,
则BO⊥AC,DO⊥AC∵平面ACD⊥平面ABC
∴DO⊥平面ABC,作EF⊥平面ABC,
那么EF∥DO,根据题意,点F落在BO上,
∴∠EBF=60,易求得EF=DO= ![]()
所以四边形DEFO是平行四边形,DE∥OF;∵DE平面ABC,OF平面ABC,∴DE∥平面ABC
(2)
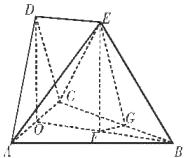
作FG⊥BC,垂足为G,连接EG;
∵EF⊥平面ABC,根据三垂线定理可知,EG⊥BC,
∴∠EGF就是二面角EBCA的平面角,
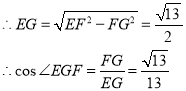 ,
,
即二面角EBCA的余弦值为![]() .
.
(3)∵平面ACD⊥平面ABC,OB⊥AC∴OB⊥平面ACD;
又∵DE∥OB∴DE⊥平面DAC,
∴三棱锥EDAC的体积![]()
又三棱锥EABC的体积![]() ,
,
∴多面体DEABC的体积为![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 过点
过点![]() 且与直线
且与直线![]() 垂直,直线
垂直,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,动点
轴对称,动点![]() 满足
满足![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,问
,问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为__________.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
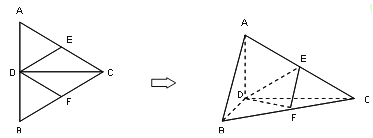
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求棱锥E-DFC的体积;
(3)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() 为坐标原点),
为坐标原点),![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com