(本小题满分13分)
证明:(Ⅰ)设A(x
1,y
1),B(x
2,y
2),由题意知AB的斜率必存在,设AB:y=kx+1,
将其代入

得:x
2-4kx-4=0,∴x
1x
2=-4…(2分)
∵

,∴

,
AM:

,化简得:AM:y=

…①
同理:BM:y=

,…②
由①②消去x得:y=

…(5分)
(Ⅱ)令F(x)=f(x)-g(x)=
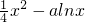
,(a>0,x>0),
∴F′(x)=
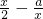
=
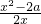
令 F′(x)=0 得x=

,
当x∈(0,

)时F′(x)<0,F(x)在x∈(0,

)上单调递减;
当x∈(

,+∞)时F′(x)>0,F(x)在x∈(

,+∞)上单调递增;
∴F(x)在

时取得最小值,…(7分)
要使f(x)≥g(x)恒成立,只需F(

)≥0
即

,解得

,又a>0,∴

…(9分)
(Ⅲ)根据(Ⅱ):取

,则有

,化简得:

…(11分)
分别令x=2,3,4,…,n,得:

,

,…,

相加:

…(13分)
分析:(Ⅰ)设AB:y=kx+1,与抛物线方程联立,求出x
1x
2,利用函数的导数推出AM,BM的斜率,得到它们的方程,然后求出点M纵坐标是一个定值即可;
(Ⅱ)构造F(x)=f(x)-g(x),求出函数的最小值,利用不等式f(x)≥g(x),说明F(x)的最小值大于等于0,即可求实数a取值范围;
(Ⅲ)利用(Ⅱ):取

,则有

,代入x=2,3,4,…,n,即可求证:
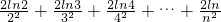
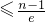
,(其中e自然对数的底数,n≥2,n∈N).
点评:本题考查函数与导数的综合应用,利用函数的最值证明不等式,直线与抛物线的位置关系的应用,考查转化数学与计算能力.

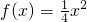 的图象C于两个不同的点A,B过点A,BC,两切线交于点M
的图象C于两个不同的点A,B过点A,BC,两切线交于点M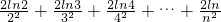
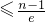 ,(其中e自然对数的底数,n≥2,n∈N).
,(其中e自然对数的底数,n≥2,n∈N). 得:x2-4kx-4=0,∴x1x2=-4…(2分)
得:x2-4kx-4=0,∴x1x2=-4…(2分) ,∴
,∴ ,
, ,化简得:AM:y=
,化简得:AM:y= …①
…① ,…②
,…② …(5分)
…(5分)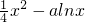 ,(a>0,x>0),
,(a>0,x>0),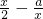 =
=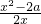
 ,
, )时F′(x)<0,F(x)在x∈(0,
)时F′(x)<0,F(x)在x∈(0, )上单调递减;
)上单调递减;  ,+∞)时F′(x)>0,F(x)在x∈(
,+∞)时F′(x)>0,F(x)在x∈( ,+∞)上单调递增;
,+∞)上单调递增; 时取得最小值,…(7分)
时取得最小值,…(7分) )≥0
)≥0 ,解得
,解得 ,又a>0,∴
,又a>0,∴ …(9分)
…(9分) ,则有
,则有 ,化简得:
,化简得: …(11分)
…(11分) ,
, ,…,
,…,
 …(13分)
…(13分) ,则有
,则有 ,代入x=2,3,4,…,n,即可求证:
,代入x=2,3,4,…,n,即可求证: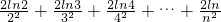
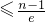 ,(其中e自然对数的底数,n≥2,n∈N).
,(其中e自然对数的底数,n≥2,n∈N).

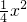 的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;
的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;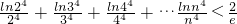 ,(其中e为无理数,约为2.71828).
,(其中e为无理数,约为2.71828). 的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;
的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值; ,(其中e为无理数,约为2.71828).
,(其中e为无理数,约为2.71828).