
【题目】已知![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)设![]() (其中
(其中![]() 为
为![]() 的导函数),判断
的导函数),判断![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ)若![]() 无零点,试确定正数
无零点,试确定正数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)单调递增;(Ⅱ) ![]() .
.
【解析】试题分析:
(1) ![]() 在定义域内恒正,则
在定义域内恒正,则![]() 在
在![]() 上单调递增.
上单调递增.
(2)结合(1)的结论分类讨论:
①当![]() 时,不符合题意;
时,不符合题意;
②当![]() 时,不符合题意;
时,不符合题意;
③当![]() 时,
时, ![]() 没有零点.
没有零点.
综上所述,正数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)因为![]() ,则
,则![]() ,
,  ,
,
所以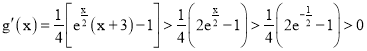 ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
(Ⅱ)由![]() 知
知![]() ,
,
由(Ⅰ)知![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,可知当
,可知当![]() 时,
时, ![]() ,
,
则![]() 有唯一零点,设此零点为
有唯一零点,设此零点为![]() .
.
易知![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增; ![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
故![]() ,其中
,其中![]() .
.
令![]() ,则
,则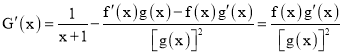 ,
,
易知![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
, ![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .
.
①当![]() 时,
时, ![]() ,由
,由![]() 在
在![]() 上单调递增知
上单调递增知![]() ,
,
则![]() ,由
,由![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 上有零点,不符合题意;
上有零点,不符合题意;
②当![]() 时,
时, ![]() ,由
,由![]() 的单调性知
的单调性知![]() ,则
,则![]() ,此时
,此时![]() 有一个零点,不符合题意;
有一个零点,不符合题意;
③当![]() 时,
时, ![]() ,由
,由![]() 的单调性知
的单调性知![]() ,则
,则![]() ,此时
,此时![]() 没有零点.
没有零点.
综上所述,当![]() 无零点时,正数
无零点时,正数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式:
(1)已知loga ![]() <1,则a>
<1,则a> ![]() ;
;
(2)函数y=2x的图象与函数y=2﹣x的图象关于y轴对称;
(3)函数f(x)=lg(mx2+mx+1)的定义域是R,则m的取值范围是0≤m<4;
(4)函数y=ln(﹣x2+x)的递增区间为(﹣∞, ![]() ]
]
正确的有 . (把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在![]() 岁的问卷中随机抽取了
岁的问卷中随机抽取了![]() 份, 统计结果如下面的图表所示.
份, 统计结果如下面的图表所示.
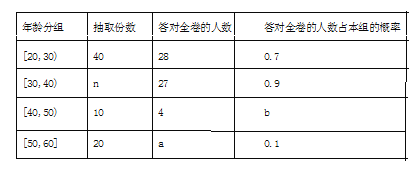
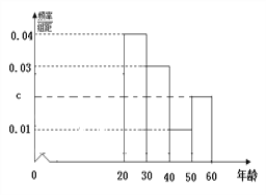
(1)分别求出![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取
答对全卷的人中随机抽取![]() 人授予“环保之星”,求年龄在
人授予“环保之星”,求年龄在![]() 的人中至少有
的人中至少有![]() 人被授予“环保之星”的概率.
人被授予“环保之星”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂每日生产一种大型产品1件,每件产品的投入成本为2000元.产品质量为一等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
(1)求在连续生产3天中,恰有一天生产的两件产品都为一等品的的概率;
(2)已知该厂某日生产的2件产品中有一件为一等品,求另一件也为一等品的概率;
(3)求该厂每日生产该种产品所获得的利润![]() (元)的分布列及数学期望.
(元)的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a≠0),记f[2](x)=f(f(x)),例:f(x)=x2+1,
则f[2](x)=(f(x))2+1=(x2+1)2+1;
(1)f(x)=x2﹣x,解关于x的方程f[2](x)=x;
(2)记△=(b﹣1)2﹣4ac,若f[2](x)=x有四个不相等的实数根,求△的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)﹣g(x)=ex , 则有( )
A.f(2)<f(3)<g(0)
B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3)
D.g(0)<f(2)<f(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com