
设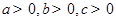 ,且
,且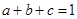 ,证明不等式:
,证明不等式: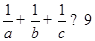
科目:高中数学 来源: 题型:解答题
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
(1)若设休闲区的长和宽的比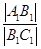 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
观察下列两个结论:
(Ⅰ)若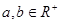 ,且
,且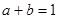 ,则
,则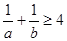 ;
;
(Ⅱ)若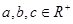 ,且
,且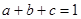 ,则
,则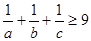 ;
;
先证明结论(Ⅱ),再类比(Ⅰ)(Ⅱ)结论,请你写出一个关于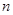 个正数
个正数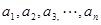 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品进货价每件50元,据市场调查,当销售价格(每件x元)为50<x≤80时,每
天售出的件数为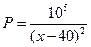 ,若要使每天获得的
,若要使每天获得的 利润最多,销售价格每件应定为多少元
利润最多,销售价格每件应定为多少元 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z= (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com