
【题目】已知函数![]() 对任意
对任意![]() ,都有
,都有![]() ,且
,且![]() 时,
时,![]() .
.
(1)求证![]() 是奇函数;
是奇函数;
(2)求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1) 证明见解析,(2)6,-6.
【解析】
(1)根据任意![]() ,都有
,都有![]() ,利用赋值法构造奇偶性判断的定义即可证明;(2)根据已知利用赋值法构造单调性的定义判断后,即可求
,利用赋值法构造奇偶性判断的定义即可证明;(2)根据已知利用赋值法构造单调性的定义判断后,即可求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
(1)证明 令x=y=0,知f(0)=0;再令y=-x,则f(0)=f(x)+f(-x)=0,所以f(x)为奇函数.
(2)解 任取x1<x2,则x2-x1>0,所以f(x2-x1)=f[x2+(-x1)]=f(x2)+f(-x1)=f(x2)-f(x1)<0.
所以f(x)为减函数.
而f(3)=f(2+1)=f(2)+f(1)=3f(1)=-6,f(-3)=-f(3)=6.
所以f(x)max=f(-3)=6,f(x)min=f(3)=-6.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四面体![]() 中,
中,![]() 分别为
分别为![]() 的中点,过
的中点,过![]() 任作一个平面
任作一个平面![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,则下列结论正确的是___________.①对于任意的平面
,则下列结论正确的是___________.①对于任意的平面![]() ,都有直线
,都有直线![]() ,
,![]() ,
,![]() 相交于同一点;②存在一个平面
相交于同一点;②存在一个平面![]() ,使得点
,使得点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上; ③对于任意的平面
的延长线上; ③对于任意的平面![]() ,都有
,都有![]() ;④对于任意的平面
;④对于任意的平面![]() ,当
,当![]() 在线段
在线段![]() 上时,几何体
上时,几何体![]() 的体积是一个定值.
的体积是一个定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.以北京为例,2018年这几类工作岗位的薪资(单位:万元/月)情况如下表所示.
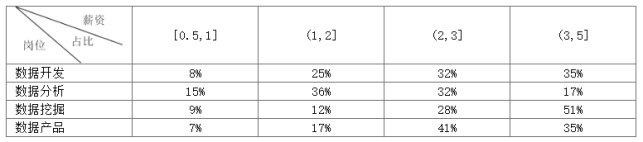
由表中数据可得各类岗位的薪资水平高低情况为
A. 数据挖掘>数据开发>数据产品>数据分析B. 数据挖掘>数据产品>数据开发>数据分析
C. 数据挖掘>数据开发>数据分析>数据产品D. 数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+![]() ,且此函数的图象过点(1,5).
,且此函数的图象过点(1,5).
(1)求实数m的值并判断f(x)的奇偶性;
(2)判断函数f(x)在[2,+∞)上的单调性,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).

(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)已知函数![]() 在
在![]() 的情况下:其在区间
的情况下:其在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.设
单调递增.设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com