
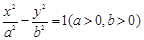 ,
,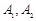 为实轴顶点,
为实轴顶点,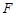 是右焦点,
是右焦点,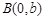 是虚轴端点,
是虚轴端点,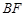 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点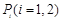 ,使得
,使得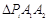 构成以
构成以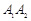 为斜边的
为斜边的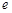 的取值范围是( )
的取值范围是( )A.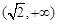 | B.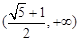 | C.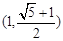 | D.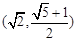 |
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源:不详 题型:单选题
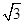 ,则C的实轴长为( )
,则C的实轴长为( )A.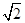 | B.2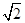 | C.4 | D.8 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
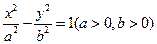 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF1⊥AF2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF1⊥AF2,原点O到直线AF1的距离为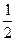 |OF1|,则双曲线的离心率为( )
|OF1|,则双曲线的离心率为( )A.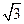 +1 +1 | B.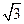 -1 -1 | C.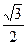 | D.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com